Ordre des éléments inversibles de Z/41Z

[Solofein]

Bonjour,

Je galère un peu pour avancer dans un exercice de maths concernant les ordres possible des éléments inversibles du groupe ,

Pour commencer je dois déterminer les ordres possibles d'un élément quelconque du groupe :

- Bon la ça va ... Je prend la liste des diviseurs de 40 ...

Mais la ou je bloque c'est pour déterminer combien d'éléments de chaque ordre ce groupe possède ...

Si quelqu'un pouvais me dire quelle propriété utiliser ou me donner un conseil ce serait génial ^^

Merci d'avance.

[Joker62]

Haileau !
Quand un élément est-il inversible dans Z/40Z ?

[Ben314]

Il y a... toute une théorie derrière...
Comme 41 est premier, F41 est un corps (commutatif) donc tout polynôme de degrés n y a au plus n racines.
Or, il s'avère que le petit théorème de fermat nous "vend" que le polynôme P(X)=X^40-1 a exactement 40 racines dans F41 (à savoir tout les éléments sauf 0).
Dans le même ordre d'idée, si tu cherche par exemple qui sont les éléments d'ordre 10 (qui divise 40), il est malin de dire que ce sont des racines du polynômes X^10-1.
Toutes les racines de X^10-1 sont elles d'ordre 10 ?
non car pour qu'un élément a soit d'ordre 10, il faut non seulement qu'il vérifie a^10=1, mais aussi que a^n soit différent de 1 pour n inférieur à 10.
Donc les éléments d'ordre 10 sont les racines de X^10-1 qui ne sont pas racines de X^5-1 ni de X^2-1 ni de X-1...

Je te laisse méditer ces pistes...

P.S. J'espère que tu n'as pas encore vu que le groupe multiplicatif d'un Fp avec p premier est cyclique, car sinon tout le travail est déjà fait...

[Solofein]

On utilise donc la liste des diviseurs de 40, à savoir :
-

Et en utilisant ce que tu viens de dire j'obtiens qu'il y a :
*1 élément d'ordre 1
*1 élément d'ordre 2
*2 éléments d'ordre 4
*1 élément d'ordre 5
*3 éléments d'ordre 8
*2 éléments d'ordre 10
*10 éléments d'ordre 20
*20 éléments d'ordre 40

Je retombe bien sur 40 éléments ... c'est correct ?



Pour le P.S. non je n'ai pas encore vu ça ... ça facilite le travail ?

[Doraki]

Moi j'ai plutôt
1 élément d'ordre 1
1 élément d'ordre 2
2 éléments d'ordre 4
4 élément d'ordre 5
4 éléments d'ordre 8
4 éléments d'ordre 10
8 éléments d'ordre 20
16 éléments d'ordre 40

Mais bon si t'es sur que t'as un élément d'ordre 40 ça veut dire que ton groupe est cyclique et isomorphe à Z/40Z, et tout de suite ça devient plus facile.

[Solofein]

Doraki, peux tu m'expliquer le raisonnement qui te permet d'arriver à ces valeurs ... j'aimerais comprendre ou est mon erreur ...

[Ben314]

Je pense que Doraki a utilisé la "théorie" qu'il y a derrière tout ça et qui donne immédiatement le nombre d'éléments d'ordre k : c'est (indicatrice d'euler) c'est à dire le nombre de nombre de {1..k} qui sont premiers avec k.

Si tu ne veut pas débaler toute la théorie, tu peut écrire :

a 40 racines qui sont les éléments d'ordre 1,2,4,5,8,10,20 ou 40
a 20 racines qui sont les éléments d'ordre 1,2,4,5,10 ou 20
a 10 racines qui sont les éléments d'ordre 1,2,5 ou 10
a 8 racines qui sont les éléments d'ordre 1,2,4 ou 8
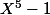
a 5 racines qui sont les éléments d'ordre 1 ou 5
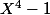
a 4 racines qui sont les éléments d'ordre 1,2 ou 4
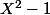
a 2 racines qui sont les éléments d'ordre 1 ou 2
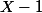
a 1 racine qui est l'élément d'ordre 1

Le fait que l'on sache que tout ces polynômes ont comme nombre de racine exactement leur degrés vient simplement du fait qu'ils divisent tous et qu'on sait (petit théorème de fermat) que ce dernier a 40 racines distinctes.

En regardant toute les informations ci dessus, et en partant du bas, tu va rapidement trouver le nombre d'éléments de chaque ordre.

[Solofein]

D'accord, merci beaucoup Doraki et Ben314 ...
Je préfère la méthode sans la théorie ;-) Plus facile à retenir.

Encore merci =)