Orbite de deux rotations de SO(3)

[busard_des_roseaux]

Bj,

On considère deux quaternions unitaires a et b.
Ce sont des points de la sphère .

Ils déterminent chacun une rotation et de l'espace euclidien
En général, ces rotations ne commutent pas.

Les rotations agissent sur la sphère , sphère unité de


soit x un point de cette sphère S2.

Si on prend des angles "simples" , du style pour R_a
et pour R_b , est-ce que l'orbite x d'un point de est finie par le sous-groupe engendré par R_a et R_b (qui ne commutent pas) ?

en fait, je ne vois pas trop et je souhaiterai que l'on m'explique ce qui se passe dans un cas simple.

[yos]

Si tu décomposes chacune de tes rotations en deux demi-tours :
,
l'axe de étant l'orthogonal des axes de et , tu as .
Tu vois alors que selon l'angle entre les axes de et , tu peux avoir n'importe quel angle entre les axes de et et donc peut être d'ordre infini.

[busard_des_roseaux]

merci.

je regarde le phénomène suivant:

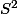
soit f une fonction continue, de domaine de définition, la sphère à valeurs dans

On regarde la nouvelle fonction définie par:


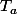
l'opérateur définit une nouvelle fonction, à partir de f,
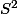
en faisant "tourner" , domaine de définition de f.

Les rotations de forment un groupe,
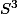
pour la composition, le groupe des déplacements de déterminant 1 , SO(3). la sphère est isomorphe à et isomorphe aussi au groupe multiplicatif des quaternions unitaires.

T_a(f) étant à valeurs réelles, on peut moyenner deux de telles applications, on définit alors la fonction:

puis l'opérateur

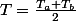
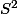
qui agit sur l'espace des fonctions continues,définies sur , à valeurs réelles.

Pour certains couples de quaternions (a,b), la suite de fonctions
a pour limite ponctuelle la fonction constante
pour toute .

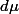
est la mesure de Lebesgue de la surface sphérique.

En effet, les pour quelconque,
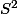
deviennent des valeurs moyennes de f sur , pour n grand.

Je me demandais si une condition nécessaire était que
soit d'ordre infini ou engendre SO(3)

(La généralisation axiomatique de cet exemple est un groupe de Lie
avec une mesure de Haar. Quelqu'un peut expliquer ?)

[yos]

Pour certains couples de quaternions (a,b), la suite de fonctions
a pour limite ponctuelle la fonction constante
pour toute .

C'est un théorème?

Je me demandais si une condition nécessaire était que
soit d'ordre infini ou engendre SO(3)

J'ai du mal à imaginer SO(3) engendré par un nombre fini de rotations.
Cela dit, le couple (Ra,Rb) peut engendrer une partie dense de SO(3) et ça peut suffire pour donner la valeur moyenne de f.
Faudrait regarder avec SO(2) déjà.