Bonjour,
J'ai fait un exercice sur l'optimisation sous contraintes et je voudrais savoir si c'est juste :
https://zupimages.net/viewer.php?id=22/42/229y.jpg
Optimisation sous contraintes.
11 messages
- Page 1 sur 1
Re: Optimisation sous contraintes.
Bonjour,
Ok pour les 2 points stationnaires.
mais pour savoir si j'étais en présence d'un maximum ou d'un minimum j'aurais écris :
f(2,1)=1/2
f(-2,-1)=-1/2
Ok pour les 2 points stationnaires.
mais pour savoir si j'étais en présence d'un maximum ou d'un minimum j'aurais écris :
f(2,1)=1/2
f(-2,-1)=-1/2
Re: Optimisation sous contraintes.
on a le théorème (de topologie) :
toute fonction continue , définie sur un ensemble compact, est bornée et atteint ses bornes.
Ici, le cercle C centré à l'origine, de rayon sqrt(5) est un fermé borné de donc compact.
donc compact.
toute fonction continue , définie sur un ensemble compact, est bornée et atteint ses bornes.
Ici, le cercle C centré à l'origine, de rayon sqrt(5) est un fermé borné de
Modifié en dernier par mathelot le 24 Oct 2022, 14:02, modifié 1 fois.
Re: Optimisation sous contraintes.
On peut vérifier tes résultats de la manière suivante:
Le cercle (C) est paramètré par:
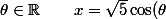 \,, \, y=\sqrt{5} \sin(\theta))
=g(\theta)=2 \sqrt{5} cos(\theta)+\sqrt{5} sin(\theta))
=5\left( \dfrac{2}{\sqrt{5}} cos(\theta)+\dfrac{1}{\sqrt{5}} sin(\theta)\right))
Il existe u réel tel que
=\dfrac{2}{\sqrt{5}} et sin(u) = \dfrac{1}{\sqrt{5}})
= 5 cos(\theta-u))
g atteint son maximum pour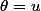 d'où
d'où 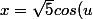=2) et
et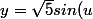 =1)
g atteint son minimum pour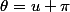 d'où
d'où 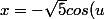=-2) et
et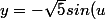 =-1)
Le cercle (C) est paramètré par:
Il existe u réel tel que
g atteint son maximum pour
g atteint son minimum pour
Re: Optimisation sous contraintes.
@phylec quand je remplace les valeurs de x et y ça me donne pas 1/2 et -1/2, dois-je prendre les valeurs de lambda comme image du coup ?
Coucou @mathelot l'énoncé du problème décrivait c comme une contrainte et non un cercle et notre professeur veut qu'on utilise la méthode des multiplicateurs de lagrange pour trouver les points critiques
Coucou @mathelot l'énoncé du problème décrivait c comme une contrainte et non un cercle et notre professeur veut qu'on utilise la méthode des multiplicateurs de lagrange pour trouver les points critiques
Re: Optimisation sous contraintes.
lisachatroux a écrit:avec ce que @phyelec a dit ?
Je n'ai rien compris à ce qu'il a écrit
Re: Optimisation sous contraintes.
Bonjour,
oups erreur ! accepter veuillez m'excuser,pas en forme hier soir , effectivement
max f(x,y)=f(2,1)=5 avec (x,y) appartient au cercle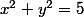
min f(x,y)=f(-2,-1)=-5 avec (x,y) appartient au cercle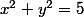
oups erreur ! accepter veuillez m'excuser,pas en forme hier soir , effectivement
max f(x,y)=f(2,1)=5 avec (x,y) appartient au cercle
min f(x,y)=f(-2,-1)=-5 avec (x,y) appartient au cercle
Re: Optimisation sous contraintes.
L'argument de compacité invoqué par mathelot est important car il évite d'utiliser des conditions du second ordre ou autres.
Imagine 5 points critiques.
Tu calcules les valeurs de f en les 5 points.
La théorie te dit:il y a un max et un min(mathelot)
Ces max et min sont atteint en des points critiques.
Donc la plus grande valeur , c'est le max et la plus petite le min.
Imagine 5 points critiques.
Tu calcules les valeurs de f en les 5 points.
La théorie te dit:il y a un max et un min(mathelot)
Ces max et min sont atteint en des points critiques.
Donc la plus grande valeur , c'est le max et la plus petite le min.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
