Bonsoir, s'il vous plaît aidez à résoudre ce problème.
Exercice
Un industriel produit simultanément 2 biens

et

dont il a le monopole de la production et de la vente dans un pays. Soit

la quantité produite du premier bien et

la quantité produite du deuxième bien. Les prix
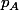
et

auxquels il vend les biens

et

sont fonctions des quantités écoulées selon les relations :
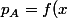)
et
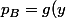)
.
Le coût de production total des quantités

et

est fonction
)
. Le bénéfice de l'entreprise si elle vend les quantités

et

est donc la fonction
=x f(x) +y g(y)-c(x ,y))
.
Trouver les quantités qui maximisent le bénéfice de l'entreprise, la valeur maximale du bénéfice ainsi que les prix de vente de chacun des biens dans le cas où
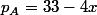
,
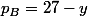
et
=x^2+3y^2+xy)
.
