MaximeD a écrit:Bonjour,
Je suis étudiant en agronomie et actuellement en stage.
La mission qui m'a été confiée est la suivante : Trouver les méthodes de calculs permettant de modifier la courbe granulométrique d'un sol en le mélangeant à d'autres granulats de différentes tailles.
J'ai trouvé une fonction (Voir pièce jointe) permettant ceci mais je n'arrive pas comprendre comment récupérer les données que je souhaite utiliser par la suite, ici la proportion en chacun des matériaux que devra posséder mon mélange pour que sa courbe granulométrique corresponde à celle souhaitée.
:mur:

Serait'il possible d'avoir de l'aide? Car je ne possède pas les connaissances suffisantes pour régler se problème.
Merci par avance
Maxime
Bonjour,
moi je vois l'image. Il ne faut pas se laisser effrayer par l'aspect matriciel du problème, l'idée derrière c'est la minimisation d'un trinôme : On a une cible D, une fonction f(x) = a*x, et on veut minimiser (D-f(x))^2 c'est à dire (D-a*x)^2 qui est un trinôme. Seulement, D est un vecteur, A une matrice, et X un vecteur, et le carré une norme 2, ce qui fait en fait un polynome de degré 2 à m variables, mais ce n'est pas plus compliqué dans l'esprit à résoudre, il faut juste annuler les dérivées.
Pour reprendre proprement,
on a :
D le vecteur objectif (granulométrie désirée du mélange ),
X le vecteur des proportions dans le melange (notre inconnue)
A la matrice de granulométrie des composants (Aij est le % de composant i qui passe dans le tamis j),
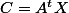
est la granulométrie du mélange (c'est la transposee de A car la granulométrie du mélange dans le tamis j est
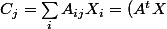_j)
on renomme
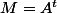
pour ne pas s'embêter avec trop de transposées dans les calculs.
on veut donc maximiser
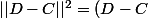^t(D-C)=(D^t-C^t)(D-C))
c'est à dire
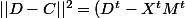(D-MX)=||D||^2-X^tM^tD-D^tMX +X^tM^tMX)
qui est un scalaire.
A partir de là, c'est bien un trinôme de degré 2 à m variables, il faut annuler les dérivées en x_i, c'est à dire annuler le gradient de la fonction. On peut revenir à l'expression sous formes de sommes et dériver classiquement selon chaque x_i en faisant attention à tous les indices, puis reconnaitre des produits matriciels dans les sommes restantes.. ou sinon directement matriciellement cela donne sauf erreur :
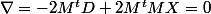
Et du coup on conclut :
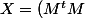^{-1}M^tD = (AA^t)^{-1}AD)
On a bien ainsi récupéré les proportions X_i à choisir de manière à minimiser la différence entre la courbe de granulométrie visée et la courbe réelle.
Damien
