Optimisation graphique
23 messages
- Page 1 sur 2 - 1, 2
Optimisation graphique
Bonjour à tous !
J'ai l'exercice suivant à faire : http://image.noelshack.com/fichiers/201 ... 155514.jpg
Voilà ce que j'ai fait : http://image.noelshack.com/fichiers/201 ... 155526.jpg
Je voulais savoir si quelqu'un pouvait confirmer que ce que j'ai fais est bon et ensuite si vous pouvez m'aider pour la dernière question car je ne vois pas comment faire
Merci à ceux qui prendront le temps de m'aider !
Cordialement
J'ai l'exercice suivant à faire : http://image.noelshack.com/fichiers/201 ... 155514.jpg
Voilà ce que j'ai fait : http://image.noelshack.com/fichiers/201 ... 155526.jpg
Je voulais savoir si quelqu'un pouvait confirmer que ce que j'ai fais est bon et ensuite si vous pouvez m'aider pour la dernière question car je ne vois pas comment faire
Merci à ceux qui prendront le temps de m'aider !
Cordialement
Re: Optimisation graphique
Salut,
Ce que tu as fait est bon.
Si tu prends la courbe de niveau C=9, peux-tu trouver un couple (x1,x2) qui respecte la contrainte R=20 ?
Ce que tu as fait est bon.
Si tu prends la courbe de niveau C=9, peux-tu trouver un couple (x1,x2) qui respecte la contrainte R=20 ?
Re: Optimisation graphique
La courbe de niveau C=9 donne 3*x1+x2 =9 donc 3*x1+x2-9=0
Donc j'aurai 3*x1+x2-9=20 soit 3*x1+ x2 =11
Et oui il y a des couples qui fonctionnent
Donc j'aurai 3*x1+x2-9=20 soit 3*x1+ x2 =11
Et oui il y a des couples qui fonctionnent
Re: Optimisation graphique
MatmatFr a écrit:Et oui il y a des couples qui fonctionnent
Alors donne-moi un couple sur la courbe de niveau C=9 qui respecte la contrainte R=20.
Re: Optimisation graphique
Le point (x1=3 ; x2= 2) n'est ni sur la courbe R=20 car 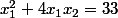 , ni sur la courbe C=9 car
, ni sur la courbe C=9 car 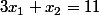
Re: Optimisation graphique
Ah d'accord alors je sais pas comment faire pour savoir si un couple marche
Re: Optimisation graphique
Ah vu que la courbe de niveau 9 ne croise pas la courbe de la contrainte ça veut dire qu'il n'y a pas de solution ?
Re: Optimisation graphique
Ça veut dire qu'il n'y a pas de solutions pour C=9. Mais pour d'autres valeurs de C ?
Re: Optimisation graphique
Je ne peux pas tester pour chaque valeur à moins qu'il n'y ait une méthode particulière non ?
Re: Optimisation graphique
Que remarques-tu sur les courbes iso-C ?
Est-ce qu'il y des solutions pour C=12 par ex ?
Est-ce qu'il y des solutions pour C=12 par ex ?
Re: Optimisation graphique
Il me semble que oui voilà ma réponse : http://image.noelshack.com/fichiers/201 ... 163022.jpg
Re: Optimisation graphique
Tu peux donc tracer la courbe C=12.
Que remarques-tu par rapport aux autres droites ? Et par rapport à la courbe R=20 ?
Que remarques-tu par rapport aux autres droites ? Et par rapport à la courbe R=20 ?
Re: Optimisation graphique
Elle est plus "haute" et elle coupe la courbe = 20 en 2 points (1;4,5) et (3,75; 0,5)
Re: Optimisation graphique
MatmatFr a écrit:Elle est plus "haute"
Oui mais il y a un truc qui doit sauter aux yeux quand tu regardes toutes les courbes iso-C.
MatmatFr a écrit:elle coupe la courbe = 20 en 2 points (1;4,5) et (3,75; 0,5)
Oui . Ça signifie que pour C=12, il y a 2 solutions qui respectent la contrainte R=20. Et bien sûr pour ces 2 solutions, le bénéfice est le même (puisque R et C sont les mêmes pour ces 2 solutions).
Pour optimiser le bénéfice, il faut diminuer C tout en restant sur la courbe R=20. Est-ce possible ?
Re: Optimisation graphique
Sa Majesté a écrit:MatmatFr a écrit:Elle est plus "haute"
Oui mais il y a un truc qui doit sauter aux yeux quand tu regardes toutes les courbes iso-C.
Honnêtement, à part que dans l'intervalle où on est elle ne coupe pas l'axe des ordonnées, rien ne me saute aux yeuxMatmatFr a écrit:elle coupe la courbe = 20 en 2 points (1;4,5) et (3,75; 0,5)
Oui . Ça signifie que pour C=12, il y a 2 solutions qui respectent la contrainte R=20. Et bien sûr pour ces 2 solutions, le bénéfice est le même (puisque R et C sont les mêmes pour ces 2 solutions).
Pour optimiser le bénéfice, il faut diminuer C tout en restant sur la courbe R=20. Est-ce possible ?
Il ne me semble pas mais je ne saurai pas dire pourquoi

Re: Optimisation graphique
Je crois avoir compris on doit avoir le minimum de C tout en touchant la courbe ce qui signifie qu'il faut trouver la courbe de niveau de C qui sera tangente à la contrainte R(x) = 20
Si c'est ça, je dois faire en tâtonnant ou il existe une méthode particulière ?
Si c'est ça, je dois faire en tâtonnant ou il existe une méthode particulière ?
Re: Optimisation graphique
MatmatFr a écrit:Je crois avoir compris on doit avoir le minimum de C tout en touchant la courbe ce qui signifie qu'il faut trouver la courbe de niveau de C qui sera tangente à la contrainte R(x) = 20
Yes !
MatmatFr a écrit:Si c'est ça, je dois faire en tâtonnant ou il existe une méthode particulière ?
Il y a une méthode de calcul mais si je me souviens bien de l'énoncé, on te demande de trouver graphiquement.
Comme toutes les courbes iso-C sont parallèles, il suffit de tracer celle qui tangente la courbe R=20 (il n'y en a qu'une, on peut le montrer par la méthode de calcul).
Re: Optimisation graphique
Ensuite je prends un point pour déterminer le niveau de la tangente et ça sera la solution du programme P, c'est bien cela ?
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
