Optimisation de fonction

[adoumbia]

Bonjour à tous je prépare mon examen de fin de semestre et je suis tombé sur un cas qui me pose problème vous pouvez m'aidez s'il vous plaît ?

Déterminer les extrema de la fonction étant donnée la contrainte suivante
f(x, y, z) =(x-2)^2-(y-1)^2+z^2
sc: x^2+y^2+z^2=5

Merci d'avance

[pascal16]

f(x, y, z) =(x-2)^2-(y-1)^2+z^2
sc: x^2+y^2+z^2=5

petites remarques :
(x-2)^2 est à maximiser, x doit être aussi loin que possible de 2 -> x va donc être proche de -sqrt(5)
-(y-1)^2 est à maximiser, y doit être aussi proche que possible de 1
z² joue un rôle contraire dans chaque cas, z=0 semble un bon candidat.

Vu le rôle prédominant de (x-2)^2, il va être très proche de -sqrt(5)

Variante 1 :
en coordonnées sphérique, f(x,y,z) sous contrainte devient f(o,phi) sans contrainte dont les dérivées partielles donne les points critiques à observer... mais par des fonctions trigo pas simples du tout

graphiquement f(-2.21, sqrt(5-2.21²),0)≃ 17.xx semble très proche du max recherché.

[mathelot]

lire ici le multiplicateurs de Lagrange:

https://fr.wikipedia.org/wiki/Multiplic ... e_Lagrange

cordialement,

[LB2]

Bonjour,

multiplicateurs de Lagrange, ou alternativement remplacer z^2 par sa valeur en fonction de x et y, et trouver les extrema sans contrainte de la fonction de deux variables obtenue.

Cordialement

[Ben314]

Salut,

Bonjour,
multiplicateurs de Lagrange, ou alternativement remplacer z^2 par sa valeur en fonction de x et y, et trouver les extrema sans contrainte de la fonction de deux variables obtenue.
Cordialement

Ca, je suis pas bien sûr que ce soit futé comme méthode : vu le niveau actuel des étudiants, une fois que la contrainte va être écrite sous la forme et que l'étudiant aura substitué dans , ben le fait qu'on continue à avoir une contrainte (à savoir ), tu peut être à peu prés sûr que ça va passer à la poubelle direct . . . (et même ceux qui comprennent qu'il reste la contrainte , ben je suis tout sauf sûr qu'ils sauront la gérer correctement)

[adoumbia]

La technique que je connais utilise le multiplicateur de lagrange je crois on a une fonction lagrangienne tq
(x-2)^2-(y-1)^2+z^2- \lambda (x^2+y^2+z^2-5)
On determine les dérivés premières qui nous permettent de déduire un système d'équations dont la solution sont les points critiques
Avec les équations je trouve aussi que z=0 mais lambda=1 du coup ça annule tout

[aviateur]

Bonjour
Moi aussi, je pense que c'est mieux de remplacer z^2 par 5-x^2+y^2.
Cela revient à minimiser h(x,y)=8 - 4 x + 2 y - 2 y^2 sur le disque de rayon racine de 5.
Comme il n'y a pas de point critique à l'intérieur du disque, les extremums sont atteints pour x^2+y^2=5.
On peut par exemple poser
On est amener à chercher les extremums d'une fonction g sur [-5,5].
Résoudre g'(x)=0 revient à savoir résoudre un polynôme de degré 3.
Un peu de courage donne
avec et (minimum)

et avec
et

[mathelot]

La technique que je connais utilise le multiplicateur de lagrange je crois on a une fonction lagrangienne tq
(x-2)^2-(y-1)^2+z^2- \lambda (x^2+y^2+z^2-5)
On determine les dérivés premières qui nous permettent de déduire un système d'équations dont la solution sont les points critiques
Avec les équations je trouve aussi que z=0 mais lambda=1 du coup ça annule tout

Comme tu connais cette méthode et que tu sais l'appliquer,fais-le. Moi, je ne peux pas t'aider plus,
car je manque de temps pour me plonger dans le Wiki

[pascal16]

L(x,y,z,λ)=(x-2)^2-(y-1)^2+z^2- λ(x^2+y^2+z^2-5)
donne après élimination de sous-cas : ( -5λ³+15λ+6=0 et z=0 avec x=2/(1-λ) et y=1/(1+λ))

[LB2]

Merci Ben! je n'avais pas fait le calcul et effectivement il restait la contrainte d'inégalité qui n'est pas simple à gérer pour un débutant

Merci aviateur, on peut aussi paramétrer le cercle de rayon racine de 5 par les formules x(t)=R*(1-t^2)/(1+t^2) et y(t)=R*2*t/(1+t^2)

Ceci dit la méthode attendue ici est probablement les multiplicateurs de Lagrange

[LB2]

Pour une solution un peu plus détaillée :

- On pose le lagrangien comme le dit Pascal,

- Les conditions du premier ordre donnent d'où par substitution

On distingue les cas (4 candidats à être des etrema locaux) et on justifie en examinant la nature de la matrice Hessienne du Lagrangien au point de coordonnées .
Ici, la matrice hessienne est simple à calculer puisqu'elle est diagonale, ses trois valeurs propres étant toutes distinctes.

Pour : toutes les valeurs propres sont strictement négatives, la hessienne est définie négative, c'est donc un max local strict
Pour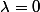 : une valeur propre est strictement négative, les deux autres strictement positives, c'est donc un point selle ou point col
Pour : une valeur propre est strictement négative, les deux autres strictement positives, c'est donc un point selle ou point col
Pour : toutes les valeurs propres sont strictement positives, la hessienne est définie positive, c'est donc un min local strict

[aviateur]

Bonjour LB2
Je ne vois pas dans la question que l'on demande d'utiliser la méthode de Lagrange. Néanmoins quelque soit la méthode utilisée, la difficulté (voire la possibilité) d'avoir les valeurs exactes est en général le même à la fin. Or personnellement j'ai fait les calculs exacts (que j'ai vérifiés perso). ¨Pour cela j'ai été amené à trouver les racines d'un polynôme de degré 3.
Ce qui n'est pas le cas pour toi.
Avec la méthode de Lagrange j'avais aussi un pol. de degré 3. Tu as dû faire une erreur.

[mathelot]

-5λ³+15λ+6=0

qui faut il croire ?

[LB2]

Bonjour LB2
Je ne vois pas dans la question que l'on demande d'utiliser la méthode de Lagrange. Néanmoins quelque soit la méthode utilisée, la difficulté (voire la possibilité) d'avoir les valeurs exactes est en général le même à la fin. Or personnellement j'ai fait les calculs exacts (que j'ai vérifiés perso). ¨Pour cela j'ai été amené à trouver les racines d'un polynôme de degré 3.
Ce qui n'est pas le cas pour toi.
Avec la méthode de Lagrange j'avais aussi un pol. de degré 3. Tu as dû faire une erreur.

Je ne vois pas comment tu peux obtenir un polynôme de degré 3 en lambda puisqu'on a une expression en x^2,y^2, et que x et y sont de degré -1 en lambda, on obtient un polynôme de degré 4 non ?
Mais 0 est racine évidente donc on retrouve un polynôme de degré 3 après élimination du cas lambda = 0 (qui donne un point selle)

@mathelot : il me semble que c'est le même polynôme modulo une erreur de signe, je pense que pascal a voulu écrire -5λ³+15λ-6=0

[pascal16]

λ≃1.905 et x=2/(1-λ) me donne bien x ≃-2.21
moi : L(x,y,z,λ)=(x-2)^2-(y-1)^2+z^2- λ(x^2+y^2+z^2-5)
lb2 : L(x,y,z,λ)=(x-2)^2-(y-1)^2+z^2 + λ(x^2+y^2+z^2-5)
donc on a en fait tous les deux raison

[aviateur]

Je ne vois pas comment tu peux obtenir un polynôme de degré 3 en lambda puisqu'on a une expression en x^2,y^2, et que x et y sont de degré -1 en lambda, on obtient un polynôme de degré 4 non ?
Mais 0 est racine évidente donc on retrouve un polynôme de degré 3 après élimination du cas lambda = 0 (qui donne un point selle)

Bon j'ai pas regardé ton polynôme qui a 0 comme valeur propre. Et finalement tu es bien ramené au même problème de calcul d'un pol de degé 3.
Dc pas de pb

[LB2]

λ≃1.905 et x=2/(1-λ) me donne bien x ≃-2.21
moi : L(x,y,z,λ)=(x-2)^2-(y-1)^2+z^2- λ(x^2+y^2+z^2-5)
lb2 : L(x,y,z,λ)=(x-2)^2-(y-1)^2+z^2 + λ(x^2+y^2+z^2-5)
donc on a en fait tous les deux raison

ben oui ça me semblait évident m'enfin