Opérations
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 02:01
par Dinozzo13 » 29 Juin 2009, 02:01
bonjour, j'ai un petit problème pour trouver le bon résultat, on donne
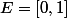
et on définit l'opération

par :
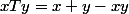
et on me demande de vérifier que

est une loi interne dans

. Je trouve

et non pas

, or

, donc

est-elle une loi interne, je dirais que oui mais j'hésite. Bref, je ne sais pas si c'est juste ou si c'est faux et pourquoi, auriez-vous une idée?, merci d'avance :ptdr:
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 29 Juin 2009, 04:17
par Zavonen » 29 Juin 2009, 04:17
Regarde d'un peu plus près:
x+y-xy <= 1 peut s'écrire x(1-y) <=(1-y)
 par busard_des_roseaux » 29 Juin 2009, 15:41
par busard_des_roseaux » 29 Juin 2009, 15:41
bonsoir,
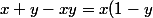+y \leq (1-y)+y \leq 1)
la loi xTy=x+y-xy ressemble à
+P(B)-P(A)P(B)=P(A)+P(B)-P(A \cap B)=P(A \Delta B))
il s'agirait donc de la probabilité d'une "différence symétrique"
entre des évênements supposés indépendants ??
Il faut voir si l'on peut effectuer ce rapprochement hasardeux.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 16:28
par Dinozzo13 » 29 Juin 2009, 16:28

donc
\le{1-y})
équivaut à
(1-y)\le{0})
,
(1-y)\ge{0})
mais après je ne vois pas :triste:
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Juin 2009, 17:14
par xyz1975 » 29 Juin 2009, 17:14
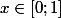
et

Donc
(y-1) \ge{0})
soit encore


Pour

positif c'est évident.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 17:23
par Dinozzo13 » 29 Juin 2009, 17:23
ok merci j'ai compris :ptdr: :++: .Après on me demande d'étudier la commutativité de T, donc, j'ai mis:
On sait que
\in{E}^{2}})
,
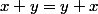
et

car
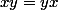
donc
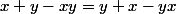
d'où
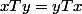
donc

est commutative dans

.
Pour l'associativité, j'ai mis :
\in{E}^{3}, (xTy)Tz=(x+y-xy)Tz=x+y-xy+z-z(x+y-xy)=x+y+z-xy-yz-xz+xyz)
, et
\in{E}^{3}, zT(yTz)=xT(y+z-yz)=x+y+z-yz-x(y+z-yz)=x+y+z-xy-yz-xz+xyz)
,
ainsi
\in{E}^{3}, (xTy)Tz=zT(yTz))
donc

est associative sur

.
Est-ce que pour l'instant tout cela paraît bien ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 19:33
par Dinozzo13 » 29 Juin 2009, 19:33
Je dois aussi démontrer d'autres propriétés de T, j'aimerais donc savoir si ce que j'ai fait jusqu'à présent est correct ou non pour savoir si je poursuis l'exrcice ou si je revoie tout cela, merci :livre: :livre:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 29 Juin 2009, 19:40
par girdav » 29 Juin 2009, 19:40
Ce que tu as fait semble correct. Je parie que les questions suivantes portent sur la recherche de l'élément neutre et de l'élément réciproque d'un élément quelconque

de

.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 19:45
par Dinozzo13 » 29 Juin 2009, 19:45
oui :ptdr: je dois étudier les propriétés de T (commutativité, associativité, élément neutre, éléments symétrisables et les éléments réguliers). J'ai fait les deux premières mais j'attendais de savoir si le peu que j'avais fait tenait la route pour connaître votre avis sur ce que j'ai fait pour les trois dernières :ptdr:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juin 2009, 20:21
par Dinozzo13 » 29 Juin 2009, 20:21
en ce qui concerne l'élément neutre, j'ai dit:

tel que

,
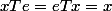
équivaut à
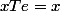
,
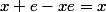
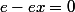
=0)
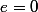
donc
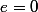
est l'élément neutre de

pour

.
Pour les éléments symétrisables,

tel que
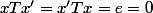
,
ça équivaut à
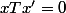
,
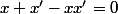
+x=0)
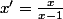
Donc tout élément de

admet un symétrique dans

pour

sous réserve que x soit différent de 1.
Et pour les éléments réguliers,
}\in{E}^{2})
,
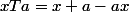
et
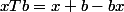
, en ajoutant membre à membre, on a,
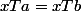
équivaut à
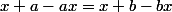
,
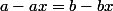
, si x différent de 1,

, donc E admet des éléments réguliers.
Qu'en dites vous ?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 29 Juin 2009, 20:48
par kazeriahm » 29 Juin 2009, 20:48
tout élement inversible est régulier
et 1 est plus que non inversible : il est absorbant
est-ce que 1 est régulier ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Juin 2009, 02:38
par Dinozzo13 » 30 Juin 2009, 02:38
alors ça j'en ai aucune idée, je dirais oui mais je ne suis pas sur :wrong:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 30 Juin 2009, 08:26
par kazeriahm » 30 Juin 2009, 08:26
que vaut 1Tx ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Juin 2009, 10:03
par Doraki » 30 Juin 2009, 10:03
C'est quoi le symétrique de 1/2 ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Juin 2009, 15:13
par Dinozzo13 » 30 Juin 2009, 15:13
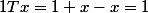
, on peut dire que 1 est absorbant.
le symétrique de 1/2 est
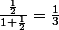
.
Mais je ne vois pas pourquoi vous me demandez de calculer 1Tx et le symétrique de 1/2, :look2:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Juin 2009, 15:24
par Doraki » 30 Juin 2009, 15:24
C'est bizarre, chez moi, (1/2)T(1/3) = 1/2 + 1/3 - 1/6 = 4/6 alors que ça devrait faire 0.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Juin 2009, 15:30
par Dinozzo13 » 30 Juin 2009, 15:30
ah nam :ptdr: , je me suis trompé de calculs à faire.
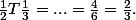
Pour quoi ça devrait faire 0 ? :doh:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Juin 2009, 15:47
par Doraki » 30 Juin 2009, 15:47
C'est quoi ta définition de symétrique d'un élément ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 30 Juin 2009, 15:53
par Dinozzo13 » 30 Juin 2009, 15:53
Pour moi un élément x est dit symétrique:
-A droite : s'il existe x' dans E tel que xTx'=e
-A gauche : s'il existe x'' dans E tel que x''Tx=e
lorsque x est symétrisable (à gauche et à droite) et si x'=x'', alors on a :
x'Tx=xTx'=e=0 .Dans ce cas x et x' sont dits symétriques pour la loi T dans E.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 30 Juin 2009, 18:20
par Doraki » 30 Juin 2009, 18:20
Bah alors pourquoi tu te demandes pourquoi (1/2) T (l'inverse de 1/2) devrait faire 0 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
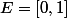 et on définit l'opération
et on définit l'opération  par :
par : 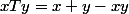 et on me demande de vérifier que
et on me demande de vérifier que  est une loi interne dans
est une loi interne dans  . Je trouve
. Je trouve  et non pas
et non pas  , or
, or  , donc
, donc  est-elle une loi interne, je dirais que oui mais j'hésite. Bref, je ne sais pas si c'est juste ou si c'est faux et pourquoi, auriez-vous une idée?, merci d'avance :ptdr:
est-elle une loi interne, je dirais que oui mais j'hésite. Bref, je ne sais pas si c'est juste ou si c'est faux et pourquoi, auriez-vous une idée?, merci d'avance :ptdr: tel que
tel que  ,
,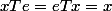 équivaut à
équivaut à 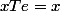 ,
,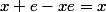
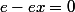
=0)
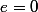
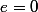 est l'élément neutre de
est l'élément neutre de  pour
pour  .
. tel que
tel que 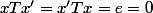 ,
,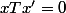 ,
,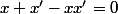
+x=0)
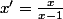
 admet un symétrique dans
admet un symétrique dans  pour
pour  sous réserve que x soit différent de 1.
sous réserve que x soit différent de 1.}\in{E}^{2}) ,
, 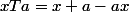 et
et 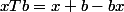 , en ajoutant membre à membre, on a,
, en ajoutant membre à membre, on a, 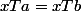 équivaut à
équivaut à 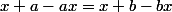 ,
, 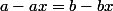 , si x différent de 1,
, si x différent de 1,  , donc E admet des éléments réguliers.
, donc E admet des éléments réguliers.