Opérations sur les polynômes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 15:53
par wilfred1995 » 10 Mar 2019, 15:53
Bonne après midi à tous
Soit
=3X^2-2, Q(X)=X^2+X-1, R(X)=aX+b.)
Calculer
*R)
et
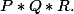
Trouver a et b afin que le degré de
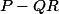
soit le plus petit possible./
2. Calculer
^5-(X-1)^5.)
3. Déterminer le degré de
^n-aX^{2n}-bX^{2n-1})
en fonction de a et b
Solution1-)
a-
P+Q 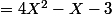
,
P*Q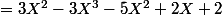
,
(P+Q)*RX^2+(-3a-b)X-3b) P*Q*R
P*Q*R 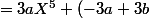X^4+(-5a-3b)X^3+(2a-5b)X^2+(2a+2b)+2b)
b-
P-QR=
X^2+(a-b)X+(b-2))
Je suis bloqué à ce niveau
j'ai eu mon idée disant que le
=0)
et que tous les coefficients doivent être nuls mais je bloque au niveau de la résolution de l'équation
merci de m'aider
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 16:03
par wilfred1995 » 10 Mar 2019, 16:03
c'est une erreur sur mon brouillon elle est bien juste désole ça bien du fait que j'ai recommencé le Latex pour la deuxieme c'etait du coup pénible

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 10 Mar 2019, 16:09
par Sa Majesté » 10 Mar 2019, 16:09
OK j'ai corrigé ton message initial.
Il y a tjs un pb avec P+Q sur le coef de X.
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 16:35
par wilfred1995 » 10 Mar 2019, 16:35
Sa Majesté a écrit:OK j'ai corrigé ton message initial.
Il y a tjs un pb avec P+Q sur le coef de X.
mais la somme de deux polynômes
P+Q, le
deg(P+Q)=max(degP, degQ) si n\neq m avec
n=degP et m=degQ mais ici ils sont égaux dont
degP=degQ
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 10 Mar 2019, 16:52
par tournesol » 10 Mar 2019, 16:52
Ton expression de P - QR te permet de repondre : il te faut diminuer son degré .
Donc a = 0 et 3 - a - b =0 .
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 17:04
par wilfred1995 » 10 Mar 2019, 17:04
ah je vois merci je bloquais au niveau de
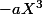
car je considérais car je prenais déjà
a=0
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 17:29
par wilfred1995 » 10 Mar 2019, 17:29
2-)
^5-(X-1)^5= 10X^4+20X^2+10X+2)
-
mathelot
 par mathelot » 10 Mar 2019, 17:36
par mathelot » 10 Mar 2019, 17:36
^5-(X-1)^5)
est paire. Don c pas de monome de degré impair
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 17:41
par wilfred1995 » 10 Mar 2019, 17:41
je ne comprends pas bien mathelot
-
mathelot
 par mathelot » 10 Mar 2019, 20:42
par mathelot » 10 Mar 2019, 20:42
posons
=(x+1)^5 - (x-1)^5)
=f(x))
pour tout x réel.
donc
^5 - (X-1)^5)
n'a pas de terme de degré impair dans son écriture.
Le terme 10X est faux
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 20:48
par wilfred1995 » 10 Mar 2019, 20:48
ok il ya une autre méthodes sans passer par les calculs très long dont j'ai procédé
-
mathelot
 par mathelot » 10 Mar 2019, 20:53
par mathelot » 10 Mar 2019, 20:53
wilfred1995 a écrit:2-)
(X+1)^5-(X-1)^5= 10X^4+20X^2+10X+2
^5-(X-1)^5= 10X^4+20X^2+2)
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 21:10
par wilfred1995 » 10 Mar 2019, 21:10
merci j'ai vu mon erreur
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 10 Mar 2019, 21:11
par wilfred1995 » 10 Mar 2019, 21:11
mathelot a écrit:^5-(X-1)^5)
est paire. Don c pas de monome de degré impair
une question s'il te plaît comment s'apercevoir que c'est paire
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 10 Mar 2019, 22:58
par tournesol » 10 Mar 2019, 22:58
mathelot t'a répondu au message 10389 .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 11 Mar 2019, 00:09
par tournesol » 11 Mar 2019, 00:09
Je me suis trompé sur l'identification des messages .
Si tu remplaces X par - X dans ton polynôme , tu dois retrouver le même polynôme .
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 11 Mar 2019, 07:20
par wilfred1995 » 11 Mar 2019, 07:20
Ok merci
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 14 Mar 2019, 05:22
par wilfred1995 » 14 Mar 2019, 05:22
3. Déterminer le degré de
^n-aX^{2n}-bX^{2n-1})
en fonction de a et b
bonjour s'il vous plaît une idée sur la dernière question
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 14 Mar 2019, 09:09
par tournesol » 14 Mar 2019, 09:09
Tu peux développer
)^n)
avec la formule du binôme .
Tu calcules le degré de chaque terme et tu pourras en déduire les termes de degré 2n ( celui la ,il est évident sans calculs ) et 2n-1 de
^n)
.
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 14 Mar 2019, 12:09
par wilfred1995 » 14 Mar 2019, 12:09
tournesol a écrit:Tu peux développer
)^n)
avec la formule du binôme .
Tu calcules le degré de chaque terme et tu pourras en déduire les termes de degré 2n ( celui la ,il est évident sans calculs ) et 2n-1 de
^n)
.
j'utilise le binôme de newton je trouve ceci:
)^n)
=
!}(X+1)(X^2)^{n-1}+.........+(X+1)^n)
Donc tout ça qui donne:
)^n-aX^{2n}-bX^{2n-1})
=
!}(X+1)(X^2)^{n-1}+.........+(X+1)^n-aX^{2n}-bX^{2n-1})
je ne vois pas concrètement où a et b vont intervenir dans le dégre de ce polynôme
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
est paire. Don c pas de monome de degré impair
en fonction de a et b
avec la formule du binôme .
.