Opérateurs sur fonctions à support fini

[Sourire_banane]

Salut,

Soit C^Z l'ensemble des fonctions de Z dans C. Supp(f) le support de f c'est l'ensemble des entiers k de Z tels que f(k) est non nul si f appartient à C^Z.

J'ai du mal à montrer que V est un sev de C^Z, V à support fini. Montrer que (0)_{C^Z} est dans V c'est fait, montrer l'inclusion aussi, mais pour la stabilité de V par + et la multiplication externe, j'ai bien stabilité par linéarité mais faut montrer que la combi linéaire est de support fini. Me vient l'idée de poser Supp(lf)=Supp(f), Supp(mg)=Supp(g), (l,m) dans C², puis de montrer que Supp(lf+mg)=Supp(f)+Supp(g), si ce n'est pas faux. Mais je ne sais pas s'il est judicieux de continuer et si tel est le cas, si la double inclusion marche à tous les coups.

J'ai ensuite montré que E est dans L(C^Z), tel que E(f)(k)=f(k+1) pour un k entier donné (l'hypothèse "E(f) appartient à C^Z si f aussi" aide). Et il me faut maintenant prouver que V est stable par E.
Cela équivaut à montrer que si l'on prend f dans V, E(f) aussi y est. Pour cela, j'ai dit que Supp(f) est fini (à n éléments), et qu'en prenant n entiers uniques qui conviennent, on peut exhiber n autres entiers (les même dont on rajoute 1) qui appartiendraient au support de E(f), et qui à eux seuls forment Supp(E(f)).
C'est juste ?

[jlb]

Salut,

Soit C^Z l'ensemble des fonctions de Z dans C. Supp(f) le support de f c'est l'ensemble des entiers k de Z tels que f(k) est non nul si f appartient à C^Z.

J'ai du mal à montrer que V est un sev de C^Z, V à support fini.
Montrer que (0)_{C^Z} est dans V c'est fait, montrer l'inclusion aussi {je comprends pas}, mais pour la stabilité de V par + et la multiplication externe, j'ai bien stabilité par linéarité mais faut montrer que la combi linéaire est de support fini. Me vient l'idée de poser Supp(lf)=Supp(f) {quand l et m ne sont pas nuls} , Supp(mg)=Supp(g), (l,m) dans C², puis de montrer que Supp(lf+mg) est contenu dans Supp(f)USupp(g){considère f, -f et l=m=1), si ce n'est pas faux. Mais je ne sais pas s'il est judicieux de continuer et si tel est le cas, si la double inclusion marche à tous les coups { tu t'en fiches: l'union de deux ensembles finis est finie}.

J'ai ensuite montré que E est dans L(C^Z), tel que E(f)(k)=f(k+1) pour un k entier donné (l'hypothèse "E(f) appartient à C^Z si f aussi" aide). Et il me faut maintenant prouver que V est stable par E.
Cela équivaut à montrer que si l'on prend f dans V, E(f) aussi y est. Pour cela, j'ai dit que Supp(f) est fini (à n éléments), et qu'en prenant les n entiers qui conviennent, on peut exhiber n autres entiers (les même dont on rajoute 1) qui forment le support de E(f).


j'ai noté qlq remarques mais c'est à vérifier, comme d'hab!!!

[Sourire_banane]

Hmmm, merci pour ton aide jlb ! J'ai oublié plein de choses en ce qui concerne l'union d'ensembles et de sev en particulier, il faut que je revoie tout ça :)

Je le dirai si j'ai pas bien compris.

[adrien69]

Un truc intéressant :

J'introduis une notation :
Soit
Si tu remarques bien, A=V

[adrien69]

Je veux dire que plutôt que de regarder une fonction de 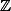dans , il suffit de regarder les coefficients de ton "polynôme" généralisé (après un petit check, je connaissais les séries de Laurent, ces polynômes ont un nom, c'est celui de "polynômes de Laurent" comme on aurait pu s'en douter).

C'est toujours plus simple de travailler avec des trucs comme ça non ?

confer

[Sourire_banane]

Ah mais attends, C[X] c'est l'ensemble des polynômes de degré indéfini (n infini) à coeffs dans C. Donc il existe dans C[X] des polynômes qui s'annulent une infinité de fois, je me trompe ?
Auquel cas, si tu engendres un ensemble qui contient de tels polynômes de Z à valeurs dans C, leur support n'est pas fini, si j'ai bien compris (ou je fais sans doute une erreur ?).

[adrien69]

Heiiiin ?
Tu cherches bien les fonctions de Z dans C qui sont nulles presque partout non, c'est-à-dire à partir d'un certain rang dans les positifs et d'un certain rang dans les négatifs ?
Auquel cas, un polynôme ce n'est rien d'autre qu'une suite de coeffs nuls à partir d'un certain rang. Donc avec mon écriture, tu vas vers les positifs et vers les négatifs, en bref, c'est pareil qu'une de tes fonctions.

D'ailleurs, t'as déjà vu un polynôme autre que le polynôme nul s'annuler une infinité de fois ?

[Doraki]

t'as l'art de compliquer les choses. après les gens vont confondre fonction polynomiale et suite des coefficients du polynome.

Supp(f) = {x / f(x) <> 0}

Supp(f+g) est inclus dans Supp(f) u Supp(g) puisque si f(x) = g(x) = 0 alors (f+g)(x) = 0.
Supp(E(f)) = {x / E(f)(x) <> 0} = {x / f(x+1) <> 0} = {x / x+1 est dans Supp(f)}, donc x -> x+1 est une bijection entre Supp(E(f)) et Supp(f), donc puisque l'un est fini, l'autre l'est aussi.

[adrien69]

Pardon monsieur.

C'était pas une solution (de ce que j'ai pu lire jlb l'avait donnée de façon correcte), juste une remarque en passant. Personnellement je trouve cette représentation plus visuelle donc meilleure. Mais c'est moi.

[Sourire_banane]

Pardon monsieur.

C'était pas une solution (de ce que j'ai pu lire jlb l'avait donnée de façon correcte), juste une remarque en passant. Personnellement je trouve cette représentation plus visuelle donc meilleure. Mais c'est moi.

Ca peut être aussi très intéressant de voir ça comme ça, même si ça ne répond pas à la question et que ça donne l'impression de passer par un autre chemin :p

En tout cas merci à tous, et à Doraki. J'ai enfin compris comment ça marche !

Enfin la partie x -> x+1 est une bijection de Supp(f) vers Supp(E(f)) je l'ai pas comprise en déduction de l'égalité de tes ensembles, Doraki.

[jlb]

Ca peut être aussi très intéressant de voir ça comme ça, même si ça ne répond pas à la question et que ça donne l'impression de passer par un autre chemin :p

En tout cas merci à tous, et à Doraki. J'ai enfin compris comment ça marche !

Enfin la partie x -> x+1 est une bijection de Supp(f) vers Supp(E(f)) je l'ai pas comprise en déduction de l'égalité de tes ensembles, Doraki.

Relis le message de Doraki: bijection de Supp(E(f)) vers Supp(f), ça va mieux comme ça :we:
{ tu pars de x dans Supp(E(f)) alors x+1 est dans Supp(f), l'application est donc bien définie et ensuite tu montres qu'elle est bijective ( injection x+1=y+1 ... surjection y dans Supp(f), considère y-1)}

[Sourire_banane]

Relis le message de Doraki: bijection de Supp(E(f)) vers Supp(f), ça va mieux comme ça :we:
{ tu pars de x dans Supp(E(f)) alors x+1 est dans Supp(f), l'application est donc bien définie et ensuite tu montres qu'elle est bijective ( injection x+1=y+1 ... surjection y dans Supp(f), considère y-1)}

Oui oui autant pour moi !

[adrien69]

Une façon de le comprendre avec les mains : quand tu indexes une suite sur Z centrer en 0, en 1, en -1 ou tout ce que tu veux ça ne change pas la face du monde.