Un opérateur génant
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Moumni
- Messages: 7
- Enregistré le: 15 Juil 2005, 11:32
-
par Moumni » 16 Juil 2005, 08:03
Salut tout le monde:
Je me pose des questions sur un opérateur integral qui m'a tant géné et il me gène encore tant que j'ai pas lui trouver la solution. L'opérateur integral dont je parle est :
F:
$)
dans
qui à tout fonction
associe
(w)=\int_{-\tau}^{\tau}\psi (x){ \frac{\sin(\sigma (w-x))}{\pi (w-x)}}dx$$)
ou
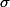
est un réel strictement positif.
Mes questions sont:
1) Un tel opérateur est_il défini positif et pourquoi?
2) Les fonctions propres d'un tel opérateur sont elles dénombrables? infini dénombrables, et pourquoi?
Et merci bien pour votre aide
Amicalement Moumni
-
Anonyme
par Anonyme » 16 Juil 2005, 12:22
Loperateur sera defini positive ssi
)}{w-x})
est positif sur tout l'intervalle I=]-T,T[ (sinon avec la caracteriqtique de l'ens ou elle est ngative on obtient le signe moins).
Ceci equivaut a
(calcul rapide)
=\frac{sin(\sigma(w-x))}{w-x})
est continue bornée sur ]-T,T[² (y compris qd w=x, cf fct holo) donc
est
)
.
Par conseq F est un operateur compact de L²(I) (thm de Kolmogorov). Donc son spectre est denombrable (car c'est un operateur hermitien de L2 ds lui-meme).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
