[MP] un opérateur fonctionnel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 02 Oct 2010, 15:25
par euler21 » 02 Oct 2010, 15:25
Bonjour
Dans un problème on définit pour les fonctions g de classe
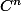
dans [-1,1] l'opérateur

défini par:
(x)=\Bigint_{0}^{1} g'(xt)dt)
pour tout
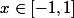
Si on se donne l'application
=xg(x))
dans ce cas il est clair que
=xg'(x)+g(x))
Est ce qu'on peut écrire dans ce cas que:
(x)=\Bigint_{0}^{1} xtg'(xt)+g(xt) dt)
Merci d'avance pour vos réponses
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2010, 15:42
par barbu23 » 02 Oct 2010, 15:42
euler21 a écrit:Bonjour
Dans un problème on définit pour les fonctions g de classe
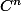
dans [-1,1] l'opérateur

défini par:
(x)=\Bigint_{0}^{1} g'(xt)dt)
pour tout
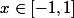
Si on se donne l'application
=xg(x))
dans ce cas il est clair que
=xg'(x)+g(x))
Est ce qu'on peut écrire dans ce cas que:
(x)=\Bigint_{0}^{1} xtg'(xt)+g(xt) dt)
Merci d'avance pour vos réponses
Salut, :happy3:
(x) = \Bigint_{0}^{1} h'(xt) dt = \Bigint_{0}^{1} xt g'(xt) + g(xt) dt $)
Donc, c'est correct :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Oct 2010, 15:47
par Ben314 » 02 Oct 2010, 15:47
Salut,
Ben, il me semble clair que oui.
Par contre, là ou l'énoncé me parrait un peu "strange", c'est que l'intégrale est triviale à calculer :
En fait Bn(g)(x)=(g(x)-g(0))/x si x non nul et Bn(g)(0)=g'(0)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2010, 15:54
par barbu23 » 02 Oct 2010, 15:54
Ben314 a écrit:En fait Bn(g)(x)=(g(x)-g(0))/x si x non nul et Bn(g)(0)=g'(0)...
Tu fais comment pour trouver ce resultat Ben ?
Merci d'avance :happy3:
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 02 Oct 2010, 15:57
par euler21 » 02 Oct 2010, 15:57
Salut Ben
effectivement ta méthode est la plus efficace pour faire ce calcul
toutefois j'ai demandé cette question juste parce que j'ai des difficultés à manipuler des intégrales chaque fois qu'on a plusieurs paramètres dedans
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2010, 16:02
par barbu23 » 02 Oct 2010, 16:02
Ben314 a écrit:Salut,
Ben, il me semble clair que oui.
Par contre, là ou l'énoncé me parrait un peu "strange", c'est que l'intégrale est triviale à calculer :
En fait Bn(g)(x)=(g(x)-g(0))/x si x non nul et Bn(g)(0)=g'(0)...
On fait le changement de variable suivant :

et donc

varie de

à

implique que

varie de

à

, et
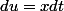
, par conséquent :
 dt = \frac{1}{x} \int_{0}^{x} g'(u) du = \frac{1}{x} (g(x) - g(0)) $)
pour

et il est clair que pour
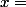
:
 = g'(0) \int_{0}^{1} dt = g'(0) $)
:happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Oct 2010, 16:21
par Ben314 » 02 Oct 2010, 16:21
Perso, j'ai juste "vu" que, si x est non nul, une primitive de t->g'(xt) est t->g(xt)/x...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
dans [-1,1] l'opérateur
défini par:
pour tout
dans ce cas il est clair que
=xg'(x)+g(x))