Notion de factorielle

par **hamster** » 29 Sep 2006, 17:31

Bonjour tout le monde ,

J'ai un petit soucis pour faire un de mes exercices de maths .

On me demande de comparer (n²)! et (n!)² .

Quelle démarche à suivre ?

Merci .

par **Imod** » 29 Sep 2006, 17:40

Il y a sûrement du Stirling la dessous .

Imod

par **abel** » 29 Sep 2006, 17:43

Sinon tu peux prendre les ln() et faire la différence des deux (qui revient a prendre le ln() du rapport)

par **nuage** » 29 Sep 2006, 17:47

Salut,
On peut regarder

et comparer le nombre de termes dans chaque produit.

par **hamster** » 29 Sep 2006, 18:20

Bonsoir ,

Imod , excuses-moi mais je n'ai rien compris à tes propos .

abel , si tu pouvais développer ton idée car pour l'instant je ne vois pas ce que le logarithme népérien vient faire là-dedans .

nuage , j'aimerais que tu me donnes plus de précision s'il te plaît .

Merci à vous .

par **Imod** » 29 Sep 2006, 18:30

hamster , c'est normal que tu n'ai rien compris car je n'ai rien fait et je n'ai pas trop le courage de faire . La formule de Stirling est une formule qui donne un équivalent de n! pour n grand .

Imod

par **abel** » 29 Sep 2006, 18:53

L'histoire du ln() c'est pour avoir une somme plutôt qu'un produit (je trouve ca + commode). La différence donne : 2*(somme de n+1 à n², ln(k)) apres on peut l'encadrer ou trouver un equivalent en +oo (la formule de stirling donne le résultat bcp + rapidement mais bon c'était une alternative)

par **hamster** » 30 Sep 2006, 09:54

Bonjour ,

Merci pour vos réponses , même si cela ne m'aide pas beaucoup ; c'était l'intention qui compte n'est-ce pas ?

nuage , peux-tu me donner plus de détails concernant ta méthode ?

Merci par avance .

par **tize** » 30 Sep 2006, 10:09

Il y a un n! au numérateur et au dénominateur que tu peux simplifier, il reste alors n! au dénominateur c'est à dire n facteurs inférieurs ou égaux à n et

facteurs (plus que n) au numérateur tous plus grand que n...

la fraction est donc plus grande que 1 d'ou

par **BancH** » 30 Sep 2006, 10:09

=> comparer (n²)! et (n!)²

par **hamster** » 01 Oct 2006, 21:22

Es-tu sûr de ce que tu racontes ?

J'ai pris une feuille de brouillon et , après avoir retourné ca dans tout les sens je ne suis toujours pas arrivé à avoir l'expression que tu as écris . :mur:

par **nuage** » 01 Oct 2006, 21:39

Salut,
Tu peux regarder sur un exemple :

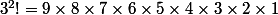
et

Notion de factorielle

Notion de factorielle

Qui est en ligne