Notation intégrale

[mainfo]

Bonjour,
Je ne sais pas si je suis dans la bonne section, mais j'ai une petite question sur la notation des intégrales. Ma question porte sur une intégrale définie d'une fonction vectorielle:
;)(de a à b) ;)(t)dt = lim (n->infini) ;) (de i=0 à n) ;)(t i *);)t
Bon c'est pas très clair à l'ordinateur...surtout pour une question de notation, mais j'apprécierais un petit peu d'aide ( dans le manuel, ils l'expliquent, mais dans le tome 1 que je n'ai pas :hum: )
Merci d'avance

[Ben314]

Salut,
Je pense que ta formule est :

C'est la définition la plus simple qui vienne à l'esprit pour l'intégrale (on approche la surface sous la courbe par des petits rectangles de largeur puis on fait tendre n vers l'infini).

Cette définition ne "marche bien" que pour des fonctions "assez régulières" (en particulier pour les fonctions continues ou continues par morçeaux sur [a,b]) mais c'est largement suffisant pour beaucoup de "cas pratiques"...

Le "coté visuel" (petit rectangles) peut donner l'impression que la définition ne marche que pour les fonction de [a,b] dans mais en fait cela marche aussi pour les fonctions de [a,b] dans 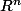car (par définition), intégrer une fonctions de [a,b] dans 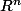revient à integrer chacunes des "coordonnées" de la fonction.