Normes et produits scalaires

[AlexisD]

Bonjour à tous.

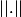
Dans un espace préhilbertien que l'on munit d'un produit scalaire , il est toujours induit de ce dernier une norme définie par:

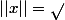
Je me souviens qu'en deuxième année, en MP, lors de la colle portant sur les espaces normés, l'enseignant m'avait demandé ce qu'était une norme. Après quelques hésitations, il a enfin lâché: C'est la racine carrée d'un produit scalaire !
Je ne sais pas pourquoi ça m'avait marqué, mais aujourd'hui j'ai des doutes là dessus: Existe-t-il des normes qui ne peuvent être induites d'un produit scalaire ? C'est à dire des espaces normés non préhilbertiens...

[Ben314]

Salut,
Que pense tu de la norme sur R² ||(x,y)||=|x|+|y| ?

[AlexisD]

Oui, j'y avais pensé. Manifestement, on ne peut pas trouvé un produit scalaire qui donne cette norme mais ya-t-il un moyen de le démontrer ?

[Doraki]

S'il y a un produit scalaire qui y corresponde,
alors pour tout x et y, N(x+y)² = N(x)² + 2 + N(y)²

Donc le produit scalaire candidat est tout indiqué, t'as juste à voir si par miracle il serait linéaire.

[AlexisD]

Ok merci bien. Effectivement, c'est plutôt simple à contredire. J'ai de quoi dire à mon ancien prof si jamais je le recroise !