Normes matricielles

[Ncdk]

Bonjour,

J'ai un exercice et j'ai du mal, c'est avec les normes matricielles.

On munit de la norme . Déterminer la norme (comme application linéaire) des matrices suivantes :

; ;

Il faut voir les matrices comme des applications en fait et prouver que ? où est une matrice constante, donc qui ne dépend pas de x et y.

[jlb]

salut, là, je ne pense pas dire de bêtise!! (enfin je crois!!)

dans l'ordre, tes normes valent 5,2 et 2

tu prends un vecteur (u,v)de R², tu calcules A (u,v) cela te donne (5u,0) dont la norme est 5||u||

tu utilises alors la définition: sup ||A(u,v)|| pour ||(u,v)||=<1 qui est donc 5 car ||(u,v)||=<1 implique ||u||=<1

[Ncdk]

D'accord merci et pour déterminer la norme de la matrice, je sais plus mais il me semble que c'est le sup de notre inégalité non ?

[MouLou]

Salut Nckd, A' n'est pas une matrice, mais une constante strictement positive.

En fait pour trouver la définition brute de la norme d'une matrice (ou d'une application linéaire),
c'est la plus petite des constantes qui vérifie C



Ou la norme E est la norme l'espace de départ, norme F est celle de l'espace d'arrivée. (Tu remarques au passage que la norme d'une matrice dépend de ces normes).

Ici tu prends la norme euclidienne pour le départ et l'arrivée.

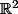
Donc du coup tu prends un vecteur (x,y) de de norme euclidienne inférieure à 1 et t'essaye de majorer la norme de A(x,y) de la manière la plus optimale possible.
Donc tu commences deja par calculer la norme de A(x,y) sachant

Petite aide: dans le cas ta norme, tu peux regarder le carré de ta norme c'est plus simple!

[Ncdk]

Ah super merci, je vais faire cette méthode même si j'ai une autre équivalente mais ça m'a l'air beaucoup plus rapide au niveau de l'étude.

Je posterai la norme de C plus tard :)

[Robot]

Plus directement : la norme de (pour la norme subordonnée à la norme de ) est



Pour calculer, puisque est de norme 1 pour la norme euclidienne standard, on peut l'écrire . Il suffit alors de prendre le sup sur .