Normes et inegalités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 19 Avr 2007, 21:00
par nemesis » 19 Avr 2007, 21:00
bonsoir
soit

=
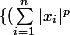 ^ 1/p , \text {si} p \in [1,\infty [ \\ \\max_ (1\le i \le n)|x_i| , \text {si} p=\infty)
je n'arrive pas ademontrer les iegalités suivantes :


et


pour n = 2 ou 3
merci pour toute aide

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 19 Avr 2007, 21:40
par nuage » 19 Avr 2007, 21:40
Salut,

semble évident.
pour

c'est pas beaucoup plus difficile, mais la j'ai un coup de flemme.
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 11:13
par nemesis » 20 Avr 2007, 11:13
pour la deuxieme inegalité est ce que c'est juste de dire :
pour n=2:
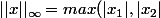)
et
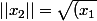^2 + (x_2)^2})
soit
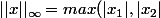=|x_1|)
alors
=|x_1| \le \sqrt{(x_1)^2 + (x_2)^2}=||x||_2)
et
^2 + (x_2)^2} \le \sqrt{(x_1)^2 + (x_1)^2} = \sqrt{2(x_1)^2} =\sqrt{2}|x_1|=\sqrt{2} ||x||_ \infty)
C.Q.F.D ?
et on fait la meme chose pour le cas ou
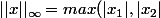=|x_2|)
?
merci d'avoir regardé
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 12:50
par nemesis » 20 Avr 2007, 12:50
alors,que ce que vous en dites ?
 par sandrine_guillerme » 20 Avr 2007, 12:53
par sandrine_guillerme » 20 Avr 2007, 12:53
ça m'a la'air juste, mais faut avouer que je viens de commencer les normes donc bon .. pas de panique lol
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 12:59
par nemesis » 20 Avr 2007, 12:59
ok ,merci
si vous avez d'autre suggestions ,n'hesitez pas !
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 20 Avr 2007, 12:59
par serge75 » 20 Avr 2007, 12:59
C'est bon nemesis
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:01
par nemesis » 20 Avr 2007, 13:01
merci ,ca avait l'air plus compliqué
maintenant ,que ce que je peux en deduire de ces inegalités ?
 par sandrine_guillerme » 20 Avr 2007, 13:01
par sandrine_guillerme » 20 Avr 2007, 13:01
j'ai une question de cours .. !
si tu as le temps , montrez que les 3 normes sont équivalents, c'est un exercice de sym de mémoire ça .. !
enfin la question n'est pas que pour nemsis ... ah tiens serge, le roi des exos, t'as une extention lol ..
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:03
par nemesis » 20 Avr 2007, 13:03
ca doit etre dans un espace vectoriel normé de dimension finie,n'est-ce pas ?
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 20 Avr 2007, 13:04
par serge75 » 20 Avr 2007, 13:04
wé.... montrer que les mêmes normes, mais définies sur l'espace R[X] des polynômes ne sont plus équivalentes.
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 20 Avr 2007, 13:06
par serge75 » 20 Avr 2007, 13:06
nemesis a écrit:ca doit etre dans un espace vectoriel normé de dimension finie,n'est-ce pas ?
Effectivement, dans un EVN de dimension finie sur R ou C, toutes les normes sont équivalentes, ce qui n'empêche pas de le montrer à la main pour ces trois là sur R^n.
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:10
par nemesis » 20 Avr 2007, 13:10
en utilisant les resultats precedent est ce que l'on a pas directement que les trois normes sont equivalentes ?
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:11
par nemesis » 20 Avr 2007, 13:11
il serait interessant de donner un contre exmple sur C([0,1],R), un volontaire ?
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:16
par nemesis » 20 Avr 2007, 13:16
moi je dirai qu'on pourait utiliser
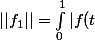| \, \mathrm dt)
et
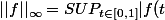|)
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 20 Avr 2007, 13:16
par serge75 » 20 Avr 2007, 13:16
fn(t)=t^n. (fn) converge pour N1 vers la fonction nulle mais pas pour la norme infinie. Ceci interdit leur équivalence.
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:19
par nemesis » 20 Avr 2007, 13:19
c'est bon ,le debat est clos ??
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
 par serge75 » 20 Avr 2007, 13:21
par serge75 » 20 Avr 2007, 13:21
Non, pas clos : je t'ai donné le contre exemple entre N1 et N-infini.
Reste à comparer N1 et N2, N2 et N_infini.
PS : dans chacun de ces deux cas, tu peux établir sur une idée analogue leur non-équivalence... je vous laisse chercher le contre exemple, la sieste m'appelle ! lol
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 20 Avr 2007, 13:28
par nemesis » 20 Avr 2007, 13:28
et si on considerait la suite
)
de E definie par
=\{ { -n^2 x + n, \text{si }x \in [0 ; 1/n] \\ 0, \text{si }x \in [1/n ; 1] })
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités