Norme et produit scalaire !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Juil 2007, 18:41
par barbu23 » 15 Juil 2007, 18:41
Bonjour:
Est ce que cette égalité existe :
soit :
 \in IR^{2} $)
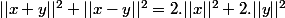
et merçi infiniment !!
Ce serait symaps si vous me donnez la démonstration de cette égalité !!
merçi d'avance !!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 15 Juil 2007, 18:47
par emdro » 15 Juil 2007, 18:47
Bonjour,
||x+y||²=(x+y)²=x²+2x.y+y².
Idem pour x-y. Tu ajoutes, et c'est gagné! :happy2:
La clé c'est ||u||²=u², le magnifique carré scalaire!
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 15 Juil 2007, 18:53
par Ledescat » 15 Juil 2007, 18:53
Bonsoir.
Tu as
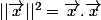
Donc
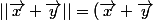^2)
(en terme de produit scalaire)
Et tu sais que tu peux développer un produit scalaire "naturellement":
^2=\vec{x}^2+\vec{y}^2+2 \vec{x}.\vec{y}\\=||x||^2+||y||^2+2 \vec{x}.\vec{y})
Je te laisse la suite :we: .
edit: grillé!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Juil 2007, 19:03
par barbu23 » 15 Juil 2007, 19:03
Ah oui, vous avez raison tous les deux ... :marteau:
On a:
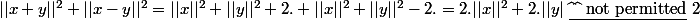
.
je l'ai trouvé dans un lien sans démonstration ,et j'avais pas le temps de reflechir, c'est pourquoi je vous ai demandé de la résoudre à ma place lol !!
:zen:
Merçi beaucoup en tous cas à vous deux "Ledescat" et "emdro" !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Juil 2007, 19:04
par barbu23 » 15 Juil 2007, 19:04
On l'appelle égalité du parallélogramme !!
-
Ledescat
- Membre Naturel
- Messages: 98
- Enregistré le: 08 Juil 2007, 15:13
-
 par Ledescat » 15 Juil 2007, 21:33
par Ledescat » 15 Juil 2007, 21:33
barbu23 a écrit:On l'appelle égalité du parallélogramme !!
Tiens je savais pas! merci aussi alors!
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 16 Juil 2007, 04:54
par BQss » 16 Juil 2007, 04:54
Ledescat a écrit:Tiens je savais pas! merci aussi alors!
Salut, d'ailleurs tu peux le visualiser geometriquement si tu veux . Prends un rectangle pour simplifier. Cette egalité resulte alors du théorème de pythagore appliqué deux fois.
Dans le rectangle ABCD:

en sommant tu obtiens:
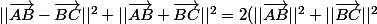^*=2||\vec{AB}||^2+2||\vec{BC}||^2)
D'où l'intitulé de la formule.
*car bien sur
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités