Nombres premiers

[BenoîtL-21]

A démontrer : Il existe une infinité de nombres premiers de la forme 4n+1.
Pour 4n+3, je l'ai prouvé par l'absurde en utilisant le fait que (4i+1)(4j+1)=4n+1, (4i+3)(4j+3)=4n+1, (4i+1)(4j+3)=4n+3 (et donc un 4n+3 non premier a toujours un 4j+3 dans sa décomposition, ce qui n'est pas vrai avec un 4n+1).
Avez-vous des idées simples pour 4n+1 ?
Merci d'avance.

[zygomatique]

salut

j'ai rien compris de ce que tu as fait ... mais ça peu éventuellement servir ...

on suppose par l'absurde que les nombres premiers de la forme 4n + 1 sont en nombre fini

on note N le quadruple du produit de ces nombres premiers augmenté de 1

il est donc de la forme N = 4p + 1

1/ N n'est divisible par aucun des premiers de la forme 4n + 1 qui ont servi à le construire

2/ si N est premier ... alors c'est fini

2/ si N n'est pas premier il est divisible par des premiers de la forme 4n + 1 ou 4n + 3

damned ... ça pourrait n'être que des 4n + 3 ....

[Ben314]

Salut,
La méthode "classique" pour les 4n+1 est légèrement plus technique :
On considère des nombres premiers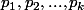 tous de la forme 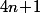et il faut montrer qu'il en existe forcément un de plus. (*)
Pour cela, on considère les entiers ainsi qu'un diviseur premier de .
- Le nombre premier peut-il être égal à 2 ? à l'un des ?
- Montre que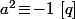 et déduis en la valeur de 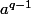modulo en fonction de la "forme" de .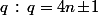
Conclue.

(*) Si tu veut tu peut raisonner par l'absurde en supposant que tu les a tous pris, mais ça n'a rien d'obligatoire vu que ça change absolument rien à ce qu'il faut démontrer par la suite : dans les deux cas (absurde ou pas) il faut montrer qu'il y en a un autre.

[Pseuda]

Bonsoir,

Pourrais-tu expliciter un peu plus la démonstration de l'infinité des nombres premiers de la forme 4n+3 ? Je ne vois pas en quoi cette explication le démontre. De mémoire on utilise un nombre formé de tous les nombres premiers de cette forme (par l'absurde, en nombre fini, p1, p2 ..., pn) : 4p1p2...pn -1, qui est divisible par un nombre pk de la forme 4n+3 (vu tes produits plus hauts), et ce n'est pas possible (ce nombre est premier avec tous les pk).

[BenoîtL-21]

Merci pour vos réponses.
@zygomatique : oui, c'est le problème, qui ne pouvait pas arriver avec 4n+3 : 4n+1 peut-être le produit de deux 4i+3, d'où mon blocage.

@Pseuda : si p1, p2, ... , pN sont les nombres premiers supposés en nombre fini de type 4n+3, alors je considère le nombre a= .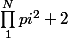
a est de type 4k+3 (cf. remarque 1er message).
Si a n'est pas premier, il est produit de nombres premiers impairs (étant impair) et (toujours cf. remarque) il y a forcément un (4k+3) (donc un pi) dans sa décomposition.
pi divise a amène pi divise 2, ce qui est absurde.
Donc a est premier et il ne fait pas partie des pi, contradiction.
Pour 4k+1, l'argument ne tient plus du fait qu'un 4k+1 peut être un produit (4i+3)(4j+3).

@ Ben314 : je suis d'accord que b est un 4k+1, et que si q divise b, alors q=4k+3.
OK aussi pour a²=-1(q) et donc .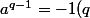
De plus q est premier, a est premier avec q, donc d'après Fermat,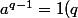 . Cela donne 1=-1 (q), ce qui est absurde, donc q n'existe pas et a est premier, différent des pi. Contradiction.
Bon, ça a l'air de marcher, non ?

Merci encore de vos réponses. A bientôt.
Benoît.