Bonjour, je suis nouveau et étudiant en Mat I
pourrais-je avoir une démonstration de lirrationalité du nombre pi (par absurde, si possible)
Nombres irrationnels
6 messages
- Page 1 sur 1
par arnaud32 » 06 Oct 2014, 12:29
jeffersson a écrit:Bonjour, je suis nouveau et étudiant en Mat I
pourrais-je avoir une démonstration de lirrationalité du nombre pi (par absurde, si possible)
http://www.google.fr/url?sa=t&rct=j&q=&esrc=s&frm=1&source=web&cd=1&cad=rja&uact=8&ved=0CCEQFjAA&url=http%3A%2F%2Fperso.univ-lemans.fr%2F~dupont%2FMaths%2FPi.pdf&ei=gHwyVJLNCsb5au-bgfgI&usg=AFQjCNE3Ncbmjuf6TbwQqXlA9PHbIoGbSA&bvm=bv.76802529,d.d2s
http://famille-chazal.pagesperso-orange.fr/somemathresults.htm
par mathelot » 06 Oct 2014, 13:00
bonjour,
supposons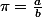
.
Posons=\frac{x^n(a-bx)^n}{n!})
(1)
Soit P , un polynome de degré
et posons:
=P(x)-P''(x)+P^{(4)}(x)+...+(-1)^nP^{(2n)}(x))
La formule de dérivée d'un produit est
=\sum_{i=0}^m \, (_i^m) \, u^{(i)}v^{(m-i)})
Lemme
(1) entraine
=R'(0)=...=R^{(n-1)}(0)=0)
=R'(\pi)=...=R^{(n-1)}(\pi)=0)
 \in \mathbb{Z},F[R](\pi) \in \mathbb{Z})
Etape2
'=P(x)sin(x))
d'où
sin(x)dx = F(0)+F(\pi))
(2)
Etape 3
on applique (2) avec P=R
^n}{n!} sin(x)dx)
 \leq \frac{a^2}{4b} \qquad \forall x \in [0;\pi])
^n \frac{1}{n!})
est une suite d'entiers strictement positifs, ne peut tendre vers zéro, quand n tend vers l'infini.
Contradiction.
Grillé par Arnaud :zen:
supposons
Posons
Soit P , un polynome de degré
La formule de dérivée d'un produit est
Lemme
(1) entraine
Etape2
d'où
Etape 3
on applique (2) avec P=R
Contradiction.
Grillé par Arnaud :zen:
par jeffersson » 07 Oct 2014, 13:06
Merci Matelo, mais y'a pas une démo plus simple? ou c'est ca la plus simple/l'unique ?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :