Nombres complexes-affixe

[Jjl]

Bonjour,on m'a donné cet exercice qui me donne du fil à retordre:
Déterminer les point M du plan dont l'affixe z vérifie (z-2)/(z+3i) appartient à R.
Alors si j'ai bien comprisje dois trouvé par exemple M(2,3) avec z=2+3i (corrigé moi si je me trompe).
Donc dans l'exercice j'ai écrit:
z=a+ib donc j'obtient: (a²+iab -3ia+iab -b+3b)/(a²+9+B²+6b)
Et b=2ab-3a ; a-2=a²+2b d'ou b=-a²-2 Mais bon je ne sais pas si ce que j'ai faisest bon mais j'aurai voulu qu'on me donne la méthode et que l'on m'explique si possible.

[chan79]

Bonjour,on m'a donné cet exercice qui me donne du fil à retordre:
Déterminer les point M du plan dont l'affixe z vérifie (z-2)/(z+3i) appartient à R.
Alors si j'ai bien comprisje dois trouvé par exemple M(2,3) avec z=2+3i (corrigé moi si je me trompe).
Donc dans l'exercice j'ai écrit:
z=a+ib donc j'obtient: (a²+iab -3ia+iab -b+3b)/(a²+9+B²+6b)
Et b=2ab-3a ; a-2=a²+2b d'ou b=-a²-2 Mais bon je ne sais pas si ce que j'ai faisest bon mais j'aurai voulu qu'on me donne la méthode et que l'on m'explique si possible.

salut


Multiplie en haut et en bas par la quantité conjuguée du dénominateur

[Jjl]

Oui c'est ce que j'ai fais,ça me donne, z-2/z+3i= (a+ib-2)(a-ib-3i)/a²+(3+b)² mais je vais détaillé ces calcule un peu plus tard parce que je dois aller en cours .
Sinon c'est la seule méthode?

[Ben314]

L'autre méthode tout aussi "classique", ça consiste à dire qu'un complexe Z donné est un réel si et seulement si il est égal à son conjugué.
Donc par exemple ici, tu partirais de . . .
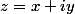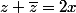Et tu utilise à la fin le fait que, si alors et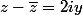
çe n'est pas fondamentalement différent de la méthode consistant à poser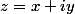 dés le départ, mais ça rend les calculs un peu moins "lourds".

On peut aussi commencer par simplifier l'expression :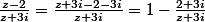 qui est réel ssi est réel, c'est à dire ssi 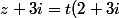avec t réel non nul.

[Jjl]

Ah ok je vois ,merci pour ton aide :)

[chan79]

en suivant ta méthode (mais c'est bien d'en voir plusieurs):


Si tu multiplies le numérateur par le conjugué du dénominateur, la partie imaginaire est
ab-(a-2)(b+3)
elle est nulle si 3a-2b-6=0
tu as ton ensemble de points M puisque que c'est l'équation d'une droite (avec un point à exclure)

[Maxmau]

Bj
Autre méthode
L'homographie T(z) = (z-2)/(z+3i) ainsi que sa réciproque, transforme une droite ou cercle du plan complexe en une droite ou un cercle. T(infini) =1 T(-3i) = infini T(2) = 0
Donc R est transformé par T^(-1) en la droite passant par 2 et -3i (cad les points (2,0) et (0,-3))

[Jjl]

Bon voila la suite de ce que j'ai posté ce matin :z-2/z+3i= (a+ib-2)(a-ib-3i)/a²+(3+b)²=a²-iab3ia+iab+b²+3b-2a+2ib+6i/a²+9+b²+6b=
a²-3ia+b²+3b-2a+2ib+6i/a²+9+b²+6b et on peut écrire que (z-2)(a²+9+b²+6b)= (a²-iab3ia+iab+b²+3b-2a+2ib+6i)(z+3i) mais en dévellopant ça je vais retombé sur quoi?
Oups j'avais pas vu ton message Chan79.

[Jjl]

Ok donc l'ensemble des point M,ce sont les point M qui vérifie l'équation de la droite?

[Jjl]

Ok ,merci pour ton aide.

[chan79]

Ok donc l'ensemble des point M,ce sont les point M qui vérifie l'équation de la droite?

oui, mais il faut enlever un point car z+3i ne peut pas être nul

[Jjl]

Ah oui c'est vrai on ne peut pas divisé un nombre par 0 mais je ne vois pas quel point je peut retiré,je peu seulement dire que z+3i doit être différent de 0 donc a+i(b+3) doit être différent de 0

[chan79]

Ah oui c'est vrai on ne peut pas divisé un nombre par 0 mais je ne vois pas quel point je peut retiré,je peu seulement dire que z+3i doit être différent de 0 donc a+i(b+3) doit être différent de 0

z doit être différent de -3i
il faut enlever le point (0,-3)
Active ce lien et place z sur la droite pour voir où se place z'

[Jjl]

Ok merci beaucoup pour ton aide chan79,tu m'a aidé a résoudre cet exercice depuis ce matin,et c'est sympa de ta part.

[chan79]

Ok merci beaucoup pour ton aide chan79,tu m'a aidé a résoudre cet exercice depuis ce matin,et c'est sympa de ta part.

De rien A+