Soit
Je voudrai savoir comment calculer le nombre de surjections possibles de
Merci infiniment ! :happy2:
Nombre de surjections possibles
11 messages
- Page 1 sur 1
Nombre de surjections possibles
par barbu23 » 20 Mar 2009, 00:18
Bonsoir à tous : :happy2:
Soit
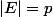
et 
:
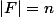
Je voudrai savoir comment calculer le nombre de surjections possibles de
dans 
!
Merci infiniment ! :happy2:
Soit
Je voudrai savoir comment calculer le nombre de surjections possibles de
Merci infiniment ! :happy2:
par barbu23 » 20 Mar 2009, 00:54
Bonjour : :happy2:
Soit $)
l'ensemble des parties de à 
éléments .
Alors : | = C_{n}^{k} $)
Ce qui fait au total :
 | = \displaystyle \sum_{k = 0}^{n} | \mathcal{P}_{k}(F) | = \displaystyle \sum_{k = 0}^{n} C_{n}^{k} = 2 ^{n} $)
Mais je ne sais pas continuer !
Un peu d'aide svp ! merci ! :happy2:
Soit
Alors :
Ce qui fait au total :
Mais je ne sais pas continuer !
Un peu d'aide svp ! merci ! :happy2:
par barbu23 » 20 Mar 2009, 17:40
Bonjour à toutes et à tous : :happy3:
Je viens de trouver sur ce lien sympas par hasard, et je le mets ici pour que vous comprenez de quoi je vais parler :
http://www.polymedia.polytechnique.fr/EnLignes/Files/08_2MathMP.pdf
Quelqu'un pourrait-t-il m'eclairer comment on fait pour trouver la formule :
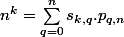
avec :
 = \begin{pmatrix} <br /> 1^1 & 1^2 & \ldots & 1^r \\ <br /> 2^1 & 2^2 & \ldots & 2^r \\ <br />\vdots & \vdots && \vdots \\ <br /> r^1 & r^2 & \ldots & r^r<br />\end{pmatrix} \hspace{150cm}<br />$)
et
 = \begin{pmatrix} <br /> p_{1,1} & p_{1,2} & \ldots & p_{1,r} \\ <br /> p_{2,1} & p_{2,2} & \ldots & p_{2,r} \\ <br />\vdots & \vdots && \vdots \\ <br /> p_{r,1} & p_{r,2} & \ldots & p_{r,r}<br />\end{pmatrix} \hspace{150cm}<br />$)
et
 = \begin{pmatrix} <br /> s_{1,1} & s_{1,2} & \ldots & s_{1,r} \\ <br /> s_{2,1} & s_{2,2} & \ldots & s_{2,r} \\ <br /> \vdots & \vdots & & \vdots \\ <br /> s_{r,1} & s_{r,2} & \ldots & s_{r,r}<br />\end{pmatrix} \hspace{150cm}<br />$)
C'est la question \hspace{3cm} a) $)
de la première partie du controle !
Merci d'avance ! :happy3:
Je viens de trouver sur ce lien sympas par hasard, et je le mets ici pour que vous comprenez de quoi je vais parler :
http://www.polymedia.polytechnique.fr/EnLignes/Files/08_2MathMP.pdf
Quelqu'un pourrait-t-il m'eclairer comment on fait pour trouver la formule :
avec :
et
et
C'est la question
Merci d'avance ! :happy3:
par barbu23 » 20 Mar 2009, 18:07
Donc, il semble que :
i.e :
 = S(r) P(r) $)
MAis e ne sais pas comment le prouver !
Merci de votre aide ! :happy3:
i.e :
MAis e ne sais pas comment le prouver !
Merci de votre aide ! :happy3:
par barbu23 » 20 Mar 2009, 18:14
D'accord, la reponse se trouve sur le lien proposé par : Nightmare !
Merci Nightmare ! :happy3:
Merci Nightmare ! :happy3:
par barbu23 » 20 Mar 2009, 20:19
Bonjour à tous : :happy3:
Je voudrais que vous m'aider un peu pour les questions de
ème partie sur ce même fil ! :happy2:
Merci d'avance ! :happy3:
Je voudrais que vous m'aider un peu pour les questions de
Merci d'avance ! :happy3:
par Purrace » 20 Mar 2009, 20:57
Du dénombrement a Polytech , eueheuehueheueeueueheheueehu (Pleurs) heureusement ces sujets , avec les sujets de geometries pures sont tres rares.(Pas difficile mais vraiment chiant!!!).
Enfin cette année , je pense qu'on aura de l'algebre lineaire (et que ca !!!!!!!!).Tu bogue à quelle question ?
Enfin cette année , je pense qu'on aura de l'algebre lineaire (et que ca !!!!!!!!).Tu bogue à quelle question ?
par barbu23 » 20 Mar 2009, 21:29
En fait ,j'ai pas encore tout lu , mais  c) $)
je ne vois pas encore comment la resoudre ! :happy3:
Merci d'avance de ton aide ! :happy2:
Merci d'avance de ton aide ! :happy2:
par barbu23 » 20 Mar 2009, 21:33
Par contre, pour  d) $)
je pense que je ai trouvé :
On a déjà trouvé que :
Donc, = A(r).P^{-1}(r) $)
Si
est inversible ! c'est ça ?
On applique la même chose por cette question non ? :hein:
C'est surtout qui me pose problème !
Merci d'avance !
On a déjà trouvé que :
Donc,
Si
On applique la même chose por cette question non ? :hein:
C'est surtout
Merci d'avance !
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :