Nombre premier de sophie germain supérieur à 10^5

[anthony_unac]

Bonjour,

Quelqu'un aurait il dans ses tiroirs la liste des nombres premiers de sophie germain de mettons 100 000 à 10 000 000 ?
Une recherche sur google (y compris en anglais) ne donne rien au dela de 100 000

Cordialement
Anthony

[Robot]

Sur les 68 906 nombres premiers entre 100 000 et 1 000 000, 6 575 sont des nombres premiers de Sophie Germain. Voici les dix derniers :
998951,
998969,
999221,
999521,
999611,
999623,
999653,
999671,
999749,
999809

[anthony_unac]

Oui le ratio est faible. Certaines personnes s'y étaient intéressées à l'époque, ils avaient même comparé ce ratio avec celui des premiers jumeaux etc ...

[Robot]

Pas si faible que ça, tout de même.
Je me pose une question : tu disposes de Maple, semble-t-il. Alors, pourquoi ne te fabriques-tu pas tes listes toi-même ?

[anthony_unac]

Oui c'est une bonne idée et à vrai dire j'ignorai que cela pouvait se coder ainsi avec un simple 'and'.
Je connaissais en revanche la fonction de base isprime(n) et également ithprime(n) qui fonctionne aussi sur wolfram.

[anthony_unac]

Dans le prolongement de cette discussion, si on souhaite travailler avec les premiers de Sophie Germain ET de Pythagore (appelons les SGP) on peut coder en utilisant le même stratagème ?

SGP:=n->isprime(n) and isprime(2*n+1) and (n =1mod(4) )

[Robot]

Sûr de la syntaxe de la dernière clause ? Vérifie tout de même.

[anthony_unac]

Point de vue syntaxe pas sur du tout vu la calamité du bonhomme en programmation (j’essaierai).
Point de vue mathématique, c'est du sûr (cf ce petit article : https://fr.wikipedia.org/wiki/Th%C3%A9o ... _de_Fermat)

[Robot]

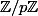
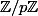
Je ne parlais pas du point de vue mathématique, qui est bien connu (un premier est somme de deux carrés si et seulement si est un carré dans si et seulement si le groupe multiplicatif de a un ordre divisible par ).

[anthony_unac]

Sûr de la syntaxe de la dernière clause ? Vérifie tout de même.

Après essai, il apparait que le code juste est :
SGP:=n->isprime(n) and isprime(2*n+1) and (1=n mod(4) )


et non pas
SGP:=n->isprime(n) and isprime(2*n+1) and (n =1mod(4) )

[Robot]

Finalement, à quoi ça t'avance d'avoir ces listes ?

[anthony_unac]

A pas grand chose si ce n'est d'avoir pu apprendre quelquechose.