Nombre parfait pair
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par busard_des_roseaux » 01 Avr 2010, 21:20
par busard_des_roseaux » 01 Avr 2010, 21:20
Bj,
vous avez une indication pour montrer qu'un entier parfait pair est de la forme
)
avec
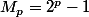
Mersenne premier
la réciproque étant niveau Terminale.
merci d'avance

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2010, 21:56
par Ben314 » 01 Avr 2010, 21:56
Si on note
)
la somme de tout les diviseurs de n (
y compris n), il est façile de vérifier que

est multiplicative, c'est à dire que,
si a et b sont premiers entre eux, on a
=\sigma(a)\sigma(b))
.
Si
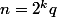
est pair (i.e.
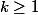
et

impair) alors
=\sigma(2^k)\sigma(q)=(2^{k+1}-1)\sigma(q))
et

est un nombre parfait ssi
=2n)
c'est à dire
\sigma(q)=2^{k+1}q\ (#))
.
Il faut donc que

divise

c'est à dire que
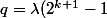)
Si

alors, comme
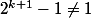
(car

),

est un diviseur propre de

est on a
\geq q+\lambda+1)
.
L'équation
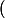)
donne alors
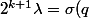\geq q+\lambda+1=\lambda(2^{k+1}-1)+\lambda+1=2^{k+1}\lambda+1)
ce qui est une belle contradiction.
On en déduit que
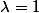
et on termine façilement.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités