DL ...nombre de derangement..!!!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 12 Mar 2008, 16:58
par mostdu95 » 12 Mar 2008, 16:58
BONJOUR
soit
= e^{-x}/(1-x))
, pour tout n on note
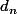
=
(0))
c'est la derivee n eme de g ,en considerabt le DL de
)
montrer que
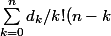!}=)
1 et montrer qu'il est egale au nombre de n derangement de n element
j'ai ecris le DL demonde : c'est
)
mais j'arrive pas a montrer l'egalite ....
aidez moi s'il vous plait et merci d'avance
 par alavacommejetepousse » 12 Mar 2008, 17:05
par alavacommejetepousse » 12 Mar 2008, 17:05
bonjour
en respectant l'indication
effectue le dl de g(x)exp(x) (formule sur le produit de dl) et identifie le avec le dl de 1 /(1-x)
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 12 Mar 2008, 17:09
par mostdu95 » 12 Mar 2008, 17:09
merci pour votre reponse..
c'est fait je l'ai met ds mon premier post mais j'arrive pas a montrer l'egalite.!! :triste:
 par alavacommejetepousse » 12 Mar 2008, 17:45
par alavacommejetepousse » 12 Mar 2008, 17:45
je ne vois pas le produit des dls dans le premier post
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 12 Mar 2008, 17:46
par mostdu95 » 12 Mar 2008, 17:46
alavacommejetepousse a écrit:je ne vois pas le produit des dls dans le premier post
c'est
)
 par alavacommejetepousse » 12 Mar 2008, 17:50
par alavacommejetepousse » 12 Mar 2008, 17:50
non ça c 'est le dl de 1/(1-x)
il faut faire celui de g(x)exp(x) en fonction des dk
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 12 Mar 2008, 18:08
par mostdu95 » 12 Mar 2008, 18:08
ahh ok bah
)
=1/(1-x )c'est une primitive de -ln(1-x)
dl de
=-(x+x^{2}/2-x^{3}/3+............+(-1)^{n-1}/n!x^{n}+o(x^{n}))
donc dl
)
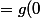-x-x²/4+.......-(-1)^{n-1}x^{n+1}/n!)
en fonction de
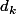
??
 par alavacommejetepousse » 12 Mar 2008, 18:37
par alavacommejetepousse » 12 Mar 2008, 18:37
il me semble que le but est une relation sur les dk...
le dl de g est donné par la formule de taylor qui fait intervenir les dk
le dl de exp est connu
fais LE PRODUIT des deux dls et c'est fini
-
mostdu95
- Membre Relatif
- Messages: 436
- Enregistré le: 09 Sep 2006, 17:36
-
 par mostdu95 » 12 Mar 2008, 21:47
par mostdu95 » 12 Mar 2008, 21:47
ah oui oui vous avez raison.....j'avais pas vu ça.!!!
 = d0+d1x+........+dn/n!+\int^{x}_{0}{x^n/n!}g^{n+1}(t)dt)
e^x= 1+x+x²/2+.........+x^n/n!+o(x^n)
dc
)
=(
(d0+d1x+........+dn/n!+\int{x^n/n!}g^{n+1}(t)dt))
=1+x+x^2+..........x^n
donc
dt=1)
par unicite de dl (j'ai developpe le premier et c'est le coeff de x^0)
mais c'est pas tout a fait ce qu'il faut montrer je sais pas où je me trompe.??
 par alavacommejetepousse » 13 Mar 2008, 10:19
par alavacommejetepousse » 13 Mar 2008, 10:19
c'est presque ça mais
il ne suffit pas de regarder le coef de x^0
il faut regarder le coeff de x^n
dans le produit on utilise la formule qui donne les coeffs du produit de deux polynômes.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités