on fait le calcul du produit du nombre complexe de module 2 et d'argument pi/3 par le nombre complexe de module 3 et d'argument -5pi/6.
la réponse est -6i
et pour le quotient on obtient -(racine 3)/3-i/3
je comprend pas comment on en arrive là...est-ce que vous pouvez me montrer les étapes intermédiaires??
une autre chose...
j'utilise O pour argument:
cos5 O=cos^5 O-10cos^3 Osin² O+5cos O sin^4 O
et
sin5 O=5cos^4 Osin O-10cos² Osin^3 O+sin^5 O
je comprend pas comment on fait...enfin je pense qu'on développe mais a la puissance 5 je comprend pas comment ça marcher...
une dernière chose ...
j'ai cos²(x)-sin²(x)=sin(3x) ssi x=pi/2 ou x=-pi/10
encore une fois je comprends pas comment on obtient ce résultat?
Nombre complexe
3 messages
- Page 1 sur 1
Salut,
1: tu peux écrire sous forme exponentielle :
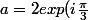\\<br />b=3exp(i\frac{ -5\pi}{6}))
le produit :
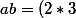*exp(i'\frac{\pi}{3}+\frac{ -5\pi}{6}))<br />=6*exp(i \frac{ -\pi}{2}))
on peut repasser en trigo :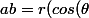+isin(\theta))) avec r =6
avec r =6
Analogue pour le quotient
2:il s'agit d'utiliser les formules de Moivre et d'Euler, en remarquant que :
^n=exp{in\theta})
cad
+isin(\theta))^n=(cos(n\theta)+isin(n\theta)))
Apres, binome Newton, puis tu isoles partie réelle si tu calcules un cos, ou Imaginaire si tu calcule un sin.
3:Un peu de trigo :-sin^2(x)=cos(2x)=sin(\frac{\pi}{2}-2x))
1: tu peux écrire sous forme exponentielle :
le produit :
on peut repasser en trigo :
Analogue pour le quotient
2:il s'agit d'utiliser les formules de Moivre et d'Euler, en remarquant que :
cad
Apres, binome Newton, puis tu isoles partie réelle si tu calcules un cos, ou Imaginaire si tu calcule un sin.
3:Un peu de trigo :
la vie est une fête 
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
