Nombre complexe, démonstration (arg)

[z^42]

Bonjour,

Je n'ai pas compris une étape de la démonstration :mur:

z=pe^(i*théta) ou {p>0, théta appartient R}

w=sigma*e^(i*gamma)

z*w=p*sigma*e^(i*(théta+gamma)

Donc Arg(zw)=gamma+sigma[2pi]= Arg(z)+Arg(w)

=> Pourquoi Arg(zw)=gamma+sigma[2pi]= Arg(z)+Arg(w) ?

Merci d'avance
Bonne journée

[zygomatique]

salut





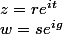
donc

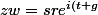arg(z) = t + m2pi
arg(w) = g + n2pi

arg(zw) = t + g + k2pi = arg(z) + arg(w) + (m + n)2pi

...

[mathelot]

ça vient:

i) soit de la série exponentielle


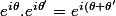qui donne par produit de convolution des séries

ii) ou du produit scalaire avec formule cos(a-b)=.. ; sin(a-b)= .. etc,

[z^42]

Bonjour

désolée du retard, merci pour vos messages

[mathelot]

re,

par produit de convolution (dit de Cauchy) des deux séries à termes complexes







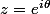
ensuite on pose pour démontrer l'ensemble de
la trigonométrie circulaire

(il y a plusieursde trigos: hyperbolique, lemniscatique, ..) qui n'ont pas été axiomatisées

en un corpus d'axiomes.