Soit n entier supérieur à 2
On suppose que piur tout facteur premier p de n, p^2 ne divise pas n mais p-1 divise n-1
Etablir que pour tout a de Z, a^n congrue à a [mod n].
Merci pour votre aide.
Nombre de Carmichael
4 messages
- Page 1 sur 1
Re: Nombre de Carmichael
Bonjour
Commence par regarder le cas où est multiple de
est multiple de  .
.
On suppose que n'est pas multiple de
n'est pas multiple de  . Montre que
. Montre que  et déduis-en que
et déduis-en que  divise
divise  .
.
Faute de frappe corrigée.
Commence par regarder le cas où
On suppose que
Faute de frappe corrigée.
Modifié en dernier par Mimosa le 14 Nov 2019, 15:56, modifié 1 fois.
Re: Nombre de Carmichael
Hum, je ne vois pas trop où va Mimosa.
On peut penser au théorème chinois. L'hypothèse que est sans facteur carré entraîne que
est sans facteur carré entraîne que 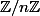 est isomorphe au produit des
est isomorphe au produit des  pour
pour  facteur premier de
facteur premier de  . Je te laisse explorer cette voie.
. Je te laisse explorer cette voie.
PS. Mimosa a corrigé une coquille, mais je ne comprends toujours pas pourquoi il ou elle cherche à démontrer l'hypothèse " divise
divise  ".
".
On peut penser au théorème chinois. L'hypothèse que
PS. Mimosa a corrigé une coquille, mais je ne comprends toujours pas pourquoi il ou elle cherche à démontrer l'hypothèse "
Re: Nombre de Carmichael
pour p facteur premier de n
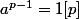
} = 1 [p]) pour tout k de N*
pour tout k de N*
comme p-1| n-1
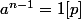
donc pour tout p facteur premier de n:
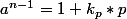
comme p^2 ne divise pas n, n est un produit de nombres premier 2 a 2 distrincts
p et q facteurs premiers de n
 donc
donc 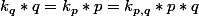 et
et 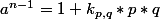
par recurence
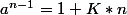
comme p-1| n-1
donc pour tout p facteur premier de n:
comme p^2 ne divise pas n, n est un produit de nombres premier 2 a 2 distrincts
p et q facteurs premiers de n
par recurence
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
