Le nom de ce theoreme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 08 Jan 2014, 12:57
par Educ » 08 Jan 2014, 12:57
bonjour,
Pourriez-vous me rappeler le nom de ce théorème ainsi sa référence sur un livre Anglo-axon et francophone
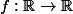
étant supposée intégrable sur

alors
ds=f(0))
je vous serais reconnaissant pour votre aide
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 08 Jan 2014, 13:01
par lionel52 » 08 Jan 2014, 13:01
Educ a écrit:bonjour,
Pourriez-vous me rappeler le nom de ce théorème ainsi sa référence sur un livre Anglo-axon et francophone
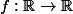
étant supposée intégrable sur

alors
ds=f(0))
je vous serais reconnaissant pour votre aide
ça s'appelle tout simplement le théorème fondamental de l'analyse!
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 08 Jan 2014, 13:08
par Educ » 08 Jan 2014, 13:08
lionel52 a écrit:ça s'appelle tout simplement le théorème fondamental de l'analyse!
pouvez-vous me fournir des références, s'il vous plaît?
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 08 Jan 2014, 13:14
par Educ » 08 Jan 2014, 13:14
merci mais si possible je veux voir ce cas exactement
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 08 Jan 2014, 13:59
par Joker62 » 08 Jan 2014, 13:59
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 08 Jan 2014, 14:08
par Educ » 08 Jan 2014, 14:08
Joker62 a écrit:ds - \int_0^0 f(s)dx}{t - 0})
merci mais Je voudrais une explication claire
-
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
 par lionel52 » 08 Jan 2014, 16:17
par lionel52 » 08 Jan 2014, 16:17
Si on note F une primitive de f
dt = F(t) - F(0))
==> THEOREME FONDAMENTAL DE LANALYSE
Donc ce que tu cherches c'est (F(t) - F(0))/t qui tend vers f(0) en 0
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 08 Jan 2014, 16:46
par Educ » 08 Jan 2014, 16:46
lionel52 a écrit:Si on note F une primitive de f
dt = F(t) - F(0))
==> THEOREME FONDAMENTAL DE LANALYSE
Donc ce que tu cherches c'est (F(t) - F(0))/t qui tend vers f(0) en 0
oui merci pourquoi nous avons F'(0)=f(0)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Jan 2014, 13:18
par Ben314 » 09 Jan 2014, 13:18
Educ a écrit:Pourriez-vous me rappeler le nom de ce théorème ainsi sa référence sur un livre Anglo-axon et francophone
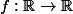
étant supposée intégrable sur

alors
ds=f(0))
Sinon, pour répondre "carré-carré" à la question, le nom de ce théorème est "je-suis-faux" : si on ne suppose pas une certaine régularité de la fonction au voisinage de 0 (par exemple f continue à droite en 0), il n'y a aucune raison que
ds)
(qui ne dépend que de la valeur de f sur tout intervalle ouvert

) soit égal à
)
.
Idem concernant la "notion de primitive" : on peut parfaitement parler de l'intégrale indéfinie d'une fonction non continue (par exemple). Dans ce cas, l'intégrale indéfinie risque fortement de ne pas être dérivable donc de ne pas être une primitive de la fonction de départ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
étant supposée intégrable sur
alors