Nbres complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maitechn
- Messages: 9
- Enregistré le: 29 Nov 2006, 19:50
-
 par maitechn » 03 Jan 2007, 11:56
par maitechn » 03 Jan 2007, 11:56
Bonjour à tous je voudrais le dévellopement de la réponse à l'expression suivante .
Atention sous la forme trigonométrique !!
( 1 + ;)2 ) + i
------------- =?
( 1 + ;)2 ) i
Merci encore.
-
khaclong
- Membre Naturel
- Messages: 10
- Enregistré le: 13 Déc 2006, 18:14
-
 par khaclong » 03 Jan 2007, 13:04
par khaclong » 03 Jan 2007, 13:04
j'ai trouvé une solution par la forme trigonométrique
On a
-1=1-2\sin^2(\frac{\pi}{8})=\cos(\frac{\pi}{4})=\frac{\sqrt2}{2})
alors
=\frac{1+\sqrt2}{2\sqrt2})
=\frac{\sqrt2-1}{2\sqrt2})
on a
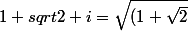^2+1} ( \frac{1+\sqrt2} { \sqrt{(1+\sqrt2)^2+1}} +\frac{i} {\sqrt{(1+\sqrt2)^2+1}}) = \sqrt{4+2\sqrt2}( \sqrt{ \frac{\sqrt2+1}{2 \sqrt2}}+i \sqrt{\frac{ \sqrt2-1}{2 \sqrt2}})=\sqrt{4+2\sqrt2}( \cos(\frac{\pi}{8})+\sin(\frac{\pi}{8})))
Par l'analogie,on a
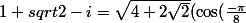+\sin(\frac{-\pi}{8})))
Donc,
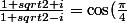+i\sin(\frac{\pi}{4})= \frac{\sqrt2}{2}+i\frac{\sqrt2}{2})
Alors ,ce probléme est résolu
-
khaclong
- Membre Naturel
- Messages: 10
- Enregistré le: 13 Déc 2006, 18:14
-
 par khaclong » 03 Jan 2007, 13:22
par khaclong » 03 Jan 2007, 13:22
Rain' a écrit:Ou alors comme j'avais dit :
(( 1 +

2 ) + i) / (( 1 +

2 ) i) = (2;)2+2)(1+i)/(2;)2+4) = (;)2+1)(1+i)/(;)2+2) =

2(1+i)/2 = cos(Pi/4)+i sin(Pi/4).
Ca me semble moins compliqué.
Qui,ta solution est moins compliqué,mais je ne montre que on peut le résoudre par la méthode trigonométrique
-
maitechn
- Messages: 9
- Enregistré le: 29 Nov 2006, 19:50
-
 par maitechn » 03 Jan 2007, 15:03
par maitechn » 03 Jan 2007, 15:03
ok merci j'ai compris , ça vérifie ce que j'avais fait.
et pour: cis 80° . (25 cis (-45°) )=?
dans les notes il trouve 5 cis 20° mais moi je trouve 25 cis (35°)
RQ : cis A = (cos A + i x sin A)
-
mathelot
 par mathelot » 03 Jan 2007, 15:30
par mathelot » 03 Jan 2007, 15:30
oui, c'est toi qui a raison. et la notation cis est ingénieuse..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
