Nbre Complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 13:40
par papino » 23 Nov 2014, 13:40
déterminer un argument et un module du nombre complexe suivant:
Z=(1-cosa+isina)/(1+cosa-isina)
hùm je sais vraiment pas comment m'y prendre pour ça
cordialement
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 13:54
par Carpate » 23 Nov 2014, 13:54
papino a écrit:déterminer un argument et un module du nombre complexe suivant:
Z=(1-cosa+isina)/(1+cosa-isina)
hùm je sais vraiment pas comment m'y prendre pour ça
cordialement
Rends le dénominateur complexe via sa quantité conjuguée
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:05
par papino » 23 Nov 2014, 14:05
je saisis pas désolé.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 14:27
par Carpate » 23 Nov 2014, 14:27
papino a écrit:je saisis pas désolé.
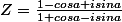
C'est pourtant ultra classique : pour isoler partie réelle et partie imaginaire de Z, il faut que son dénominateur soit rendu réel. Pour cela on multiplie le nominateur et le dénominateur de Z par la quantité conjuguée du dénominateur (ainsi on ne modifie pas la valeur de Z)
Je te laisse remplir les ...
- la quantité conjuguée de

est ....
- le produit de

par sa quantité conjuguée est le réel .......
- l'expression de Z devient ....
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:31
par papino » 23 Nov 2014, 14:31
la quantité conjuguée: 1+cosa+isina
le produit: (1+cosa)²+sina²
ça va jusque la?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 14:31
par Carpate » 23 Nov 2014, 14:31
papino a écrit:la quantité conjuguée: 1+cosa+isina
le produit: (1+cosa)²+sina²
ça va jusque la?
oui, tu peux réduire : (1+cosa)²+sina²
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:38
par papino » 23 Nov 2014, 14:38
oui ça donne 2+2cosa
j'ai à la fin Z=(cosa+2isina)/2+2cosa
ça va?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 14:46
par Carpate » 23 Nov 2014, 14:46
papino a écrit:oui ça donne 2+2cosa
j'ai à la fin Z=(cosa+2isina)/(2+2cosa) attention aux parenthèses !
ça va?
Je trouve
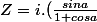)
sauf erreur ...
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:50
par papino » 23 Nov 2014, 14:50
oui tu as raison j'ai vu l'erreur j'avais oublié un -cosa
maintenant je dois transformer ça sous la forme a+bi? ou mon nombre complexe est un imaginaire pur?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 14:50
par Carpate » 23 Nov 2014, 14:50
Carpate a écrit:Je trouve
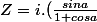)
sauf erreur ...
Et ça se simplifie encore en passant à l'arc moitié
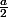
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:53
par papino » 23 Nov 2014, 14:53
hùm sec okey je le simplifie
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:54
par papino » 23 Nov 2014, 14:54
j'ai trouvé Z=i(sina/2)/(cos²a/2) c'est bon?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 14:56
par Carpate » 23 Nov 2014, 14:56
papino a écrit:j'ai trouvé Z=i(sina/2)/(cos²a/2) c'est bon?
c'est plutôt :
Z = i . sin(a/2) / (cos(a/2) = ...
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 14:57
par papino » 23 Nov 2014, 14:57
les fonctions "arc" ne sont pas dans mon programme
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 15:01
par Carpate » 23 Nov 2014, 15:01
papino a écrit:les fonctions "arc" ne sont pas dans mon programme
C'était façon de parler sur le cercle trigonométrique arc et angle au centre ont la même mesure
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 15:09
par papino » 23 Nov 2014, 15:09
ah oui c'est vrai maintenant comment je transforme ce que j'ai?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 15:11
par Carpate » 23 Nov 2014, 15:11
papino a écrit:ah oui c'est vrai maintenant comment je transforme ce que j'ai?
c'est quoi ton résultat final ?
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 15:14
par papino » 23 Nov 2014, 15:14
j'ai Z=i(sina)/(1+cosa) ou encore Z=i(sina/2)/(cos²a/2)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 23 Nov 2014, 15:19
par Carpate » 23 Nov 2014, 15:19
papino a écrit:j'ai Z=i(sina)/(1+cosa) ou encore Z=i(sina/2)/(cos²a/2)
Oui pour le début, non pour le "ou encore"
1+cosa = ...
-
papino
- Membre Naturel
- Messages: 72
- Enregistré le: 13 Sep 2014, 16:30
-
 par papino » 23 Nov 2014, 15:22
par papino » 23 Nov 2014, 15:22
1+cosa= 1+(2cos²a/2 -1)=2cos²a/2? et sina=2sina/2 cosa/2
tout ceci donne alors tana/2?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
