Bonsoir,
je dois déterminer la nature de l'intégrale sin(pi/x)/(x(1-x))^(3/2) dx sur l'intervalle [0, 1]
Au voisinage de 0, j'ai dit que c'était équivalent a (pi*x)/(x^3/2) = pi/x^(1/2) donc d'après Riemann, il ya convergence.
Est ce que cela vous parait bien?
Au voisinage de 1, je suis bloqué...
J'ai dit que c'est équivalent a sin(pi*x)/(1-x)^(3/2) mais après ça, je ne sais pas quoi faire...
Qu'en pensez vous? Merci.
Nature d'une intégrale
11 messages
- Page 1 sur 1
Re: Nature d'une intégrale
Bonjour En 1 le problème est le même quand 0 puisqueta fonction est "symétrique" par rapport à 1/2; i.e f(x)=f(1-x)
comme en zéro c'est OK en 1 aussi
comme en zéro c'est OK en 1 aussi
Re: Nature d'une intégrale
Oui mais un raisonnement de ce genre ne me suffit pas. Il faut que je le prouve à la bêbete comme ci je ne l'avais pas fait au voisinage de 0
Re: Nature d'une intégrale
Salut,
P.S. Dans l'énoncé, c'est sin(pi.x)/... ou bien sin(pi/x)/... ? (vu ce que tu écrit ensuite, ça donne l'impression que c'est pi.x sauf que ce que tu as écrit au début, c'est pi/x ...)
Sauf que... c'est complètement faux vu que lorsque x tend vers 0, t=pi/x tend vers +oo et sin(t) n'est absolument pas équivalent à t.lightone a écrit:Au voisinage de 0, j'ai dit que c'était équivalent a (pi*x)/(x^3/2) = pi/x^(1/2)...
P.S. Dans l'énoncé, c'est sin(pi.x)/... ou bien sin(pi/x)/... ? (vu ce que tu écrit ensuite, ça donne l'impression que c'est pi.x sauf que ce que tu as écrit au début, c'est pi/x ...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Nature d'une intégrale
c'est sin(pi*x)/ .. Ca n'est pas faux puisque pi*x converge vers 0 quand x tend vers 0. Donc on peut utiliser le DL et c'est donc équivalent à pi*x pour le numérateur. Et pour le dénominateur, (1*(1-x))^(3/2) est bien équivalent a x^(3/2) puisqu'on peut remplacer l'un des x par 0 sans soucis. On a donc bien à la fin que c'est équivalent à (pi)/x^(1/2) et puisque 1/2 est strictement inférieur à 1, d'après Riemann et au voisinage de 0, ça converge.
Re: Nature d'une intégrale
Si l'énoncé exact, c'est sin(pi.x)/... alors c'est O.K.
Sauf que c'est pas ça que tu as écrit dans ton post :
Sauf que c'est pas ça que tu as écrit dans ton post :
lightone a écrit:Bonsoir,
je dois déterminer la nature de l'intégrale sin(pi/x)/(x(1-x))^(3/2) dx sur l'intervalle [0, 1]
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Nature d'une intégrale
Rebonjour
A la "bêbete" j'espère que cela ne veut pas dire bêbete, c'est à dire mettre se mettre des oeillères. Car on fait des math non?
C'est à dire que l'on ne peut pas interdire toute solution pour en avoir une.
Bref tu fais ce que tu veux, tu a fais un dl en x=0 et puis tu veux faire de même en x=1.
Mais faire un DL en 1 est équivalent à faire un Dl u=0 en ayant posé u=1-x.
Tu te mets donc des oeillères et bêtement tu vas refaire le même travail!!!
C'est ça que tu veux??


Oui mais un raisonnement de ce genre ne me suffit pas. Il faut que je le prouve à la bêbete comme ci je ne l'avais pas fait au voisinage de 0
A la "bêbete" j'espère que cela ne veut pas dire bêbete, c'est à dire mettre se mettre des oeillères. Car on fait des math non?
C'est à dire que l'on ne peut pas interdire toute solution pour en avoir une.
Bref tu fais ce que tu veux, tu a fais un dl en x=0 et puis tu veux faire de même en x=1.
Mais faire un DL en 1 est équivalent à faire un Dl u=0 en ayant posé u=1-x.
Tu te mets donc des oeillères et bêtement tu vas refaire le même travail!!!
C'est ça que tu veux??



Re: Nature d'une intégrale
Aviateur, pour avoir déja fait ce genre d'exo, c'est bien ta deuxième option qu'il faut faire. Par contre, dans le sinus, ça ne converge pas vers 1 mais vers pi au voisinage de 1 donc s'il fallait faire un changement de variable, ça ne serait pas celui là. D'ou mon problème car avec un changement de variable, ça ne marcherait pas.
Re: Nature d'une intégrale
Je ne comprends ce que tu dis.
Ma deuxième option c'est la première, non?
tu poses x=1-u , donc f(x)=f(1-u)=f(u) et quand x tend vers 1, u tends vers 0.
Mais le DL de f en u=0, tu l'as déjà fait donc la nature de l'intégrale en x=1
est bien le même qu'en u=0.
Il n' y a pas 36 options. Le fait que f(x)=f(1-x) c'est une aubaine et tu ne peux pas y échapper?
Ma deuxième option c'est la première, non?
tu poses x=1-u , donc f(x)=f(1-u)=f(u) et quand x tend vers 1, u tends vers 0.
Mais le DL de f en u=0, tu l'as déjà fait donc la nature de l'intégrale en x=1
est bien le même qu'en u=0.
Il n' y a pas 36 options. Le fait que f(x)=f(1-x) c'est une aubaine et tu ne peux pas y échapper?
Re: Nature d'une intégrale
J'ai déja fait plein d'exos où on devait travailler au voisinage de 0 et de 1 et on a jamais dit que comme au voisinage de 0 ça converge, au voisinage de 1, ça converge aussi. Et les seuls fois où on a fait un changement de variable, c'est lorsque qu'on avait sin(x) où x converge vers 1 mais que pour utiliser le DL, le x doit converger vers 0 donc on faisait le changement de variable. C'est tout.
Re: Nature d'une intégraleC'est
Bon! maintenant pour que l'on se comprenne on va faire des phrases intelligibles sinon c'est la galère.
Je répète : On sait que l'intégrale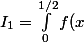 dx) est convergente et que pour tout
est convergente et que pour tout 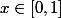 on a f(x)=f(1-x).
on a f(x)=f(1-x).
On en déduit donc que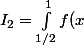 dx) est convergente puisque le changement de variable
est convergente puisque le changement de variable 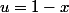 dans
dans 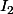 conduit à
conduit à 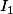
Je répète : On sait que l'intégrale
On en déduit donc que
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
