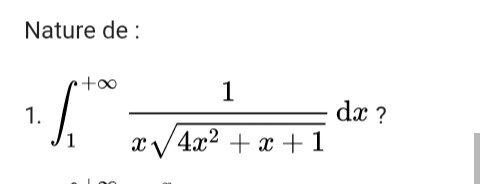Nature d'une intégrale généralisée.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
par Georges10 » 10 Avr 2019, 08:23
Bonjour à tous j'espère que vous allez bien.
Voici, il y'a un petit problème que j'ai avec la détermination de la nature d'une intégrale généralisée.
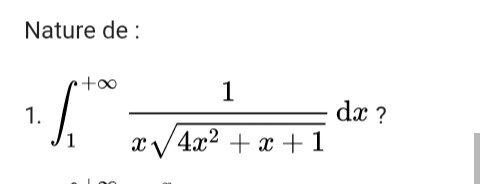
En fait, j'ai cherché et j'ai trouvé que la fonction est négligeable devant (1/x). Et comme intégrale de 0 à +oo de (1/x) est divergente , j'en déduis que l'intégrale citée en haut au debut est divergente.
Cependant il me semble qu'il y'a quelque chose qui cloche.
Merci d'avance !
-
Rdvn
- Habitué(e)
- Messages: 840
- Enregistré le: 05 Sep 2018, 11:55
-
par Rdvn » 10 Avr 2019, 09:09
Bonjour
La fonction à intégrer est définie, continue et POSITIVE sur [1,+infini[, vous pouvez donc utiliser le critère d’équivalence : sous le radical, mettez 4x^2 en facteur , il est alors facile de trouver un équivalent en +infini
et de montrer la convergence de cette intégrale.
D'autre part,et c'est peut être le plus important, votre raisonnement est totalement faux :
si pour f et g deux fonctions positives sur un intervalle et telles que f<g , l'intégrale de g est +infini, vous ne pouvez simplement rien conclure...
(même supposant f et g continues pour ne pas se perdre dans les détails)
bon courage
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
par Georges10 » 10 Avr 2019, 11:40
Ah OK je vois, donc je pense qu'en prenant (1/x^ 2) ça marche.
-
aviateur
par aviateur » 10 Avr 2019, 11:57
Bonjour
Si on désigne f(x) la fonctions sous le signe somme, fais attention à ce que tu dis.
"qu'en prenant (1/x^ 2) ça marche" c'est pas très jojo.
Au voisinage de
on a
\sim \dfrac{1}{2x^2})
En fait ce qui m'intéresses c'est la valeur exacte de l'intégrale.!!
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
par Georges10 » 10 Avr 2019, 14:48
En fait, il y'a une propriété qui dit que si f et g sont deux fonctions continues qui sont équivalentes, elles ont la même nature c-a-d soit convergentes soit divergentes. Mais cette propriété ne dit rien sur la valeur de l'intégrale généralisée.
Puisqu'il était question de déterminer la nature de l'intégrale généralisée, c'est pourquoi j'ai pris (1/x^ 2).
Mais je sais intégrale de 0 à +oo de (1/2x^2) = 0.
-
aviateur
par aviateur » 10 Avr 2019, 14:50
Ok mais fait attention tout de même il faut aussi que les deux fonctions gardent un signe constant.
D'autre part si le calcul n'est pas demandé c'est simplement une remarque que j'ai faite. ça fait partie des questions qu'on pourra te demander plus tard.
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
par Georges10 » 10 Avr 2019, 18:44
Mais comme vous le dites, si on me demandait la valeur de l'intégrale généralisée, je ne vois pas trop.
Est ce que je peux attribuer la valeur de l'intégrale généralisée (1/2x^2) à celle dont il est question ?
Merci pour votre réponse.
-
aviateur
par aviateur » 10 Avr 2019, 19:21
Non pas du tout. La comparaison montre qu'elle est convergente. Mais c'est tout.
Maintenant il y a des intégrales convergentes dont on sait calculer la valeur exacte d'autres non.
Celle ci on peut la calculer mais je n'ai plus le temps ce soir pour expliquer. c'est pas très compliqué
mais un peu long.
Si ça t'intéresse quelqu'un peut peut être le faire ou je le ferai +plus tard.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 10 Avr 2019, 19:56
Bonsoir aviateur
Je suis preneur car je l'ai calculée (
)
Mais au prix de 3 changements de variables !!!et de longs et fastidieux calculs
-
mathelot
par mathelot » 10 Avr 2019, 21:45
-
aviateur
par aviateur » 10 Avr 2019, 22:02
Bonsoir
@tournesol a priori je ne vois qu'une seule façon de faire (surement ce que tu as fait).
Etape 1 Se ramener à la forme canonique
Etape 2. Faire le changement de variable X=sinh(u) pour tuer la racine carrée.
On se retrouve alors en une fraction rationnelle de
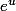
. Le changement
finira le travail.
Le seul problème c'est un peu long (pas à la main) mais à recopier.
Voici le début :
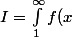 dx)
forme canonique avec X=
=\dfrac{4}{\sqrt{15} x \sqrt{1+\left(\frac{1}{\sqrt{15}}+\frac{8 x}{\sqrt{15}}\right)^2}})
Alors
.)
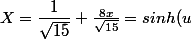Le changement de variable donne donc
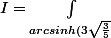}^{\infty} \dfrac{4 \sqrt{15}}{15 \sinh(u)-\sqrt{15}})
Puis faire z=e^u, la fraction rationnelle n'est pas trop horrible.... à finir (évidemment
) est à simplifer))
pour trouver
))
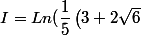Modifié en dernier par aviateur le 10 Avr 2019, 22:52, modifié 5 fois.
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
par Georges10 » 10 Avr 2019, 22:12
OK merci pour vos réponses. Si je comprend bien le but est de déterminer une primitive de la fonction et de calculer sa limite en +oo.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 10 Avr 2019, 22:22
Merci aviateur
je ne sais pas ce qui m'est arrivé mais au lieu d'exprimer shu à l'aide d'exp u , j'ai posé z=th (u/2) ...
-
aviateur
par aviateur » 10 Avr 2019, 22:46
Mais ça marche aussi. Tu dois arriver au même
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 11 Avr 2019, 08:12
Bien sûr que ça marche puisque c'est avec ce changement que j'ai trouvé , mais bonjour les calculs :
Les changements de variables entrainent des calculs sur les bornes.
Mes changements sont
,
)
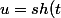puis enfin
)
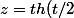pour la borne 1 , cela donne
puis
)
Avec la formule
)=\frac{\sqrt{1+x^2}-1}{x})
on obtient la borne
puis le calcul à la main de
\right]_{\frac{4\sqrt{6}-\sqrt{15}}{9}}^1=\frac{3+2\sqrt{6}}{5})
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 11 Avr 2019, 08:16
J'ai oublié ln et je viens de lire ta modification . Merci aviateur .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
