Bonjour,
Les partiels arrivent à grand pas, et je suis pas très fort niveau calcul d'intégrale. Pourriez vous me donnez les réponses pour savoir la nature de ces intégrales en x ( divergentes, semi-convergentes ou
absolument convergentes ) avec une explication claire pour que je comprennes bien la méthode à utiliser ?
L'intégrale de 0 à +infini de sin(1/x^2)
L'intégrale de 0 à +infini de 1/(sqrt(e^(x) - 1 )
L'intégrale de 1 à +infini de sqrt(4x^9 + 2x^2 - 5 ) - 2x^3
L'intégrale de 0 à +infini de ln((x^2)/(x^2 + 2 )) * sin(racine cubique de u)
L'intégrale de 1 à 2 de ( sqrt( ln(x) ) ) / (x-1)
L'intégrale de 1 à +infini de cos(x)/x^t avec t>0
Je vous remercie pour vos indications, le partiel c'est lundi.
Nature d'Integrale
20 messages
- Page 1 sur 1
Re: Nature d'Integrale
par mathelot » 04 Déc 2020, 20:08
bonsoir,
Intégrale 1
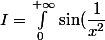 dx)
On fait le changement de variable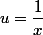
il vient:
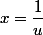
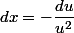
}{u^2} du)
}{u^2}| \leq \dfrac{1}{u^2})
En
f est intégrable.
En u=0}{u^2})=1)
f est donc intégrable au voisinage de 0.
l'intégrale I est absolument convergente.
Intégrale 1
On fait le changement de variable
il vient:
En
En u=0
f est donc intégrable au voisinage de 0.
l'intégrale I est absolument convergente.
Re: Nature d'Integrale
par mathelot » 04 Déc 2020, 21:56
Intégrale 2
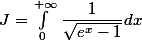
il manque une parenthèse: L'intégrale de 0 à +infini de 1/(sqrt(e^(x) - 1 )).
On fait le changement de variable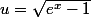
il vient:
)
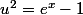
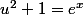
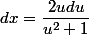
} du)
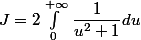
]_{0}^{+\infty}=\pi)
l'intégrale J est absolument convergente.
il manque une parenthèse: L'intégrale de 0 à +infini de 1/(sqrt(e^(x) - 1 )).
On fait le changement de variable
il vient:
l'intégrale J est absolument convergente.
Modifié en dernier par mathelot le 07 Déc 2020, 12:10, modifié 1 fois.
Re: Nature d'Integrale
par mathelot » 04 Déc 2020, 22:08
intégrale 3
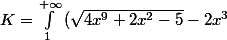 dx)
pour x assez grand:
l'intégrande tend vers
, l'intégrale K est divergente
pour x assez grand:
l'intégrande tend vers
Modifié en dernier par mathelot le 06 Déc 2020, 23:31, modifié 1 fois.
Re: Nature d'Integrale
par Arthuroua » 04 Déc 2020, 22:45
Je te remercie pour ton aide et effectivement l'intégrale 4 c'est :
L'intégrale de 0 à +infini de ln((x^2)/(x^2 + 2 )) * sin(racine cubique de x)
L'intégrale de 0 à +infini de ln((x^2)/(x^2 + 2 )) * sin(racine cubique de x)
Re: Nature d'Integrale
par mathelot » 04 Déc 2020, 22:49
intégrale 5
}}{x-1}dx)
Le problème se situe au voisinage de 1.
on pose)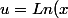
, il vient:
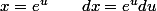
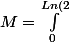} \, \dfrac{\sqrt{u}e^u}{e^u-1}du)
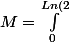} \, \dfrac{ue^u}{\sqrt{u}(e^u-1)}du)
quand u tend vers zéro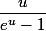
tend vers 1 (inverse du nombre dérivé de l'exponentielle en 0)
quand u tend vers zéro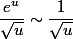
cette dernière fonction est intégrable au voisinage de 0.
M est donc une intégrale absolument convergente (l'intégrande est de signe constant)
Le problème se situe au voisinage de 1.
on pose
quand u tend vers zéro
quand u tend vers zéro
cette dernière fonction est intégrable au voisinage de 0.
M est donc une intégrale absolument convergente (l'intégrande est de signe constant)
Modifié en dernier par mathelot le 06 Déc 2020, 23:32, modifié 1 fois.
Re: Nature d'Integrale
par Arthuroua » 05 Déc 2020, 10:00
Merci pour tes explications, il ne reste plus que la 4 et la 6. Je vais m'entrainer sur d'autres intégrales.
Re: Nature d'Integrale
par Arthuroua » 05 Déc 2020, 21:13
Tu aurais quoi du coup pour la 4 et la 6 ?
Re: Nature d'Integrale
par mathelot » 05 Déc 2020, 21:54
Arthuroua a écrit:Tu aurais quoi du coup pour la 4 et la 6 ?
On va démarrer l'étude de la (6)
intégrale 6
soit t >0
le problème est en
as tu avancé ?
il s'agirait de montrer que l'intégrale N converge, et ce, absolument si t >1, simplement si
Re: Nature d'Integrale
par Arthuroua » 06 Déc 2020, 09:58
Non j'ai fais que des entrainements sur d'autres intégrales
Re: Nature d'Integrale
par Arthuroua » 06 Déc 2020, 10:34
Je pourrais avoir une correction comme tu l'as fais pour les autres parce que ca m'a vraiment aidé pour comprendre d'autre intégrale hier.
Re: Nature d'Integrale
par mathelot » 06 Déc 2020, 16:39
J'ai un empêchement, je peux pas t'aider.
Pour la (6), pour t>1, Majore abs(cos x) par 1.
Pour 0<t<=1, fais une intégration par parties, poser u'=cos x, u=sin x, v=x^(-t).
Si tu veux montrer que l'intégrale est divergente en valeur absolue, minore le cosinus en valeur absolue sur 3pi/4+k pi, 5pi/4+kpi par rac(2)/2 et x^(-t) par (5pi/4+k pi) ^(-t), ce qui fait une série en k divergente.
Pour la (6), pour t>1, Majore abs(cos x) par 1.
Pour 0<t<=1, fais une intégration par parties, poser u'=cos x, u=sin x, v=x^(-t).
Si tu veux montrer que l'intégrale est divergente en valeur absolue, minore le cosinus en valeur absolue sur 3pi/4+k pi, 5pi/4+kpi par rac(2)/2 et x^(-t) par (5pi/4+k pi) ^(-t), ce qui fait une série en k divergente.
Modifié en dernier par mathelot le 06 Déc 2020, 23:09, modifié 1 fois.
Re: Nature d'Integrale
par mathelot » 06 Déc 2020, 19:44
Pour t>1,
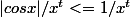
x->x^(-t) donne une intégrale absolument convergente à l'infini.
Pour 0<t<=1 intégrons par parties
On pose u'=cos x, u=sin x, v=x^(-t), v'=-tx^(-t-1)
D'où
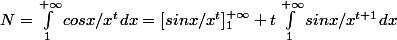
Cette dernière intégrale converge.
L'intégrale N est donc convergente.
On peut montrer que N n'est pas absolument convergente
x->x^(-t) donne une intégrale absolument convergente à l'infini.
Pour 0<t<=1 intégrons par parties
On pose u'=cos x, u=sin x, v=x^(-t), v'=-tx^(-t-1)
D'où
Cette dernière intégrale converge.
L'intégrale N est donc convergente.
On peut montrer que N n'est pas absolument convergente
Modifié en dernier par mathelot le 06 Déc 2020, 23:11, modifié 3 fois.
Re: Nature d'Integrale
par mathelot » 06 Déc 2020, 21:01
Montrons que l'intégrale 6 n'est pas absolument convergente si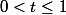 
:
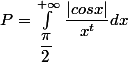
lemme: si la fonction f prend des valeurs positives , alors pour tout sous-ensembles de
A et B (mesurables), alors
si
alors  dx \leq \int_{B} f(x) dx)
^t})
Cette dernière série de la variable k est divergente. P est donc une intégrale non absolument convergente.
lemme: si la fonction f prend des valeurs positives , alors pour tout sous-ensembles de
si
Cette dernière série de la variable k est divergente. P est donc une intégrale non absolument convergente.
Modifié en dernier par mathelot le 06 Déc 2020, 23:28, modifié 1 fois.
Re: Nature d'Integrale
par mathelot » 06 Déc 2020, 22:55
Pour l'intégrale 4
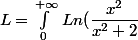 sin(\sqrt[\frac{1}{3}](x)) dx)
Il y a deux problèmes, en x=0 et en
en x=0
Lemme: dx)
est convergente pour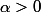 
1ère méthode: l'intégrande est négative et bornée en x=0. Elle admet un prolongement par continuité . Elle est intégrable au voisinage de 0.
2ème méthode: intégration par parties:
 dx= [\dfrac{ x^{\alpha+1}}{\alpha+1} Ln(x)]_{x=0}^{x=1} -\int_{0}^{1} \, \dfrac{x^{\alpha}}{\alpha+1} dx)
La dernière intégrale est convergente, les termes de bord sont nuls.
étudions l'intégrale R définie par
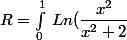 sin(\sqrt[\frac{1}{3}](x)) dx)
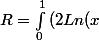- Ln(x^2+2)) sin(\sqrt[\frac{1}{3}](x)) dx)
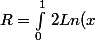 sin(\sqrt[\frac{1}{3}](x)) dx- \int_{0}^{1} \, Ln(x^2+2)) sin(\sqrt[\frac{1}{3}](x)) dx)
Les deux intégrandes sont continues en x=0 . R est donc une intégrale convergente en x=0.
en étudions l'intégrale
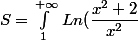 sin(\sqrt[\frac{1}{3}](x)) dx)
 =Ln(1+\dfrac{2}{x^2}) \sim \dfrac{2}{x^2})
L'intégrale S est donc absolument convergente en
Il y a deux problèmes, en x=0 et en
en x=0
Lemme:
1ère méthode: l'intégrande est négative et bornée en x=0. Elle admet un prolongement par continuité . Elle est intégrable au voisinage de 0.
2ème méthode: intégration par parties:
La dernière intégrale est convergente, les termes de bord sont nuls.
étudions l'intégrale R définie par
Les deux intégrandes sont continues en x=0 . R est donc une intégrale convergente en x=0.
en
L'intégrale S est donc absolument convergente en
Re: Nature d'Integrale
par mathelot » 06 Déc 2020, 23:34
Bonne nuit. 
je croise les doigts pour ton partiel
je croise les doigts pour ton partiel
Re: Nature d'Integrale
par mathelot » 09 Déc 2020, 01:02
j'ai traité principalement les exercices avec l'intégrale de Riemann. On peut se demander si, avec l'intégrale de Lebesgue, certains calculs se simplifient , voire même deviennent obsolètes .
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :