Multiplier dx par f(x) ça a un sens ?

[Larxane]

Bonjour, je suis en pleine préparation pour mes examens, et il y a une question qui m'interpelle dans un exercice de résolution d'équation de la chaleur.
Je ne comprend pas la solution donnée ci-dessous :


Je sais que df/dt=f'(t), et que la dérivée partielle selon x est δf/δt, mais comment je peux en arriver à dire que δt*f(t)=f'(t) ?? C'est peut-être tout simple mais j'ai beau réfléchir je ne vois pas comment on peut en arriver à un tel raisonnement...

Merci et bonne journée à vous

[Ben314]

Salut,
Je ne comprend pas le sens de la question et encore moins les deux passages en rouge suivants :

Je sais que df/dt=f'(t), et que la dérivée partielle selon x est δf/δt, mais comment je peux en arriver à dire que δt*f(t)=f'(t) ??

Le morceau de solution que tu montre, tout ce qu'il utilise, c'est le fait que, quand on dérive la quantité par rapport à la variable , le est une constante.
Ensuite, que la dérivée de la quantité par rapport à la variable ce soit ben c'est la définition même de ce qu'est une dérivée partielle, non ?

[Larxane]

Salut,
Je ne comprend pas le sens de la question et encore moins les deux passages en rouge suivants :

Je sais que df/dt=f'(t), et que la dérivée partielle selon x est δf/δt, mais comment je peux en arriver à dire que δt*f(t)=f'(t) ??

Le morceau de solution que tu montre, tout ce qu'il utilise, c'est le fait que, quand on dérive la quantité par rapport à la variable , le est une constante.
Ensuite, que la dérivée de la quantité par rapport à la variable ce soit ben c'est la définition même de ce qu'est une dérivée partielle, non ?

C'est le δt(f(t)g(x)) que je ne comprends pas, je n'ai jamais vu de δt autre part que dans l'expression δf(t)/δt du coup je ne comprend pas comment dans la correction on passe de δt(f(t)g(x)) à f'(t)g(x)...
Pour le contexte je n'ai pas fait de maths depuis la terminale il y a... 7 ans. Du coup la question peut paraitre bête mais ça m'échappe...

[Ben314]

Ah, O.K.
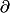
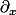
Bon, déjà, c'est pas un δ (delta : lettre grecque) mais un ("d" rond) et, visiblement, pour allèger le laïus, le bouquin dont est tiré l'exo. utilise les notation et pour les dérivées partielles premières et seconde en .
Les notations et sont peut-être un peu plus fréquente que celles là (encore que...), mais bon, comme disait je sais plus qui, les mathématiques sont invariantes à changement de notation prés . . .
Et il me semble que, vu le contexte, même si on n'a jamais vu ces notations, on peut se douter de ce qu'elles signifient, non ?

P.S. : En plus, visiblement ces notations ne sont pas que dans la correction : l'équation aux dérivées partielle de l'énoncé est aussi écrite avec ces notations là.