mathelot a écrit: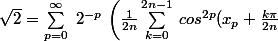 \right))
je cite cette série en précisant plusieurs points
i) on ne sait pas, à l'heure actuelle si
est un nombre normal en base 2
içi ii)
dans la série de Taylor qui donne
on dispose de nombreux "degrés de liberté"
- pour chaque entier
considéré de la série, on peut choisir
arbitrairement l'entier n=n(p) pour effectuer la moyenne des puissances
de cosinus et l'on peut aussi choisir arbitrairement, pour chaque entier p,
le réel x=x(p) dans le cosinus.
La série s'écrit:
} \sum_{k=0}^{2n(p)-1} \, cos^{2p}(x(p) + \frac{k \pi}{2n(p)}) \right))
iii) de plus, comme on moyenne
)
termes entre 0 et 1, la moyenne appartient à [0;1] et cette moyenne, qui vaut
}{2^{2p}})
est donc un nombre décimal de l'intervalle ]0;1[
iv)
De plus, quand l'entier n(p) est choisi arbitrairement grand,
la somme des cosinus est une somme de Riemann et a donc pour
limite l'intégrale:
dt)
ça fait donc beaucoup de degrés de liberté,
l'idée :id: serait donc de choisir astucieusement, à chaque indice p de sommation, pourquoi pas par récurrence sur l'entier p, le réel x(p) et l'entier naturel n(p)>p , de manière à prouver que
est un nombre normal en base 2.
Donc je sors l'exponentielle de la somme. 