Morphisme de C - algèbres

[barbu23]

Bonjour à tous,

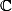
J'aimerais que vous m'aidiez à trouver un isomorphisme ( ou simplement un morphisme ) de - algèbres : qui respecte les transformations suivantes :




On peut remarquer à priori que : et, , et , sont linéairement indépendant.

Merci d'avance. :happy3:

[L.A.]

Bonsoir.

Si tu prends l'image de la matrice

010
002
300

d'après la deuxième condition ce doit être elle-même, mais d'après la première ce doit être

030
001
200

donc ça n'existe pas. En fait tes conditions sont clairement incompatibles, puisque tu veux agir de trois façons différentes sur la MEME matrice.

[barbu23]

Merci. :happy3:
J'ai oublié de préciser que et et sont trois nombres fixes ( ce ne sont pas des variables qui changent et )
Merci de prendre ça en compte. :happy3:
Merci d'avance. :happy3:

[barbu23]

Voiçi ce que je reçois comme réponse sur un autre forum "anglophone" :

All those three matrices share the same set of eigenvalues. If it is possible to find a linear transformation such that it maps the eigenspaces of the second matrix to themselves, and interchanges the eigenspaces of the other two, then conjugating by should do the trick. –

Pouvez vous me le traduire ? Je n'ai pas un bon niveau en anglais.

Merci d'avance. :happy3:

[barbu23]

Voiçi ce que je reçois comme réponse sur un autre forum "anglophone" :

All those three matrices share the same set of eigenvalues. If it is possible to find a linear transformation such that it maps the eigenspaces of the second matrix to themselves, and interchanges the eigenspaces of the other two, then conjugating by should do the trick. –

Pouvez vous me le traduire ? Je n'ai pas un bon niveau en anglais.

Merci d'avance. :happy3:

[L.A.]

OK,

All those three matrices share the same set of eigenvalues. If it is possible to find a linear transformation such that it maps the eigenspaces of the second matrix to themselves, and interchanges the eigenspaces of the other two, then conjugating by should do the trick.

"Ces trois matrices ont le même ensemble de valeurs propres. S'il est possible de trouver une transformation linéaire P qui envoie les espaces propres de la seconde matrice sur eux-même, et échange les espaces propres des deux autres, alors la conjugaison par P devrait marcher."

Après, là comme ça de but en blanc, je peux pas te dire si ça marche ou pas...