Bonjour,
Je suis entrain de faire un exercice où le but et de montrer l'équivalence de proposition.
J'ai presque fini mais il me manque une implication pour conclure.
Voici l'exercice:
Soit N et N' deux normes de l'espace vectoriel V, montrer l'équivalence des propriétés suivantes.
(a) l'identité de V est continue en tant qu'application de (V,N) dans (V,N')
(b) l'application N' est continue de (V,N) dans R
(c) l'application de la (b) est lipchitzienne
(d) N domine N'
J'ai réussi les applications :
(a) ==> (b)
(b) ==> (c)
(d) ==> (a)
Mais je n'arrive pas à montrer que (c) implique (d).
Merci d'avance pour votre aide.
Montrer une implication entre deux normes
11 messages
- Page 1 sur 1
Re: Montrer une implication entre deux normes
Bonjour
Je ne comprends pas pourquoi tu as un problème. En effet (c) implique (d) c'est direct (une évidence) alors que il y a au moins une implication dans tout ça qui est difficile.
Alors je me pose la question suivante: tu peux exprimer (c) puis (d) ? pour voir
Je ne comprends pas pourquoi tu as un problème. En effet (c) implique (d) c'est direct (une évidence) alors que il y a au moins une implication dans tout ça qui est difficile.
Alors je me pose la question suivante: tu peux exprimer (c) puis (d) ? pour voir
Re: Montrer une implication entre deux normes
Pour (c) N' application de (V,N) dans R lipschitzienne cela donne:
Pour tout x,y appartenant à V il existe K une constante strictement positive telle que
| N'(x) - N'(y) | K * N(x-y)
K * N(x-y)
et pour (d) N domine N'
Pour tout v appartenant à V il existe une constante C strictement positive telle que
N'(v) C * N(v)
C * N(v)
Pour tout x,y appartenant à V il existe K une constante strictement positive telle que
| N'(x) - N'(y) |
et pour (d) N domine N'
Pour tout v appartenant à V il existe une constante C strictement positive telle que
N'(v)
Re: Montrer une implication entre deux normes
Je viens de penser à quelque chose, si je prend y = 0, j'ai alors
|N'(x) - N'(0)| K * N(x-0)
K * N(x-0)
comme N' est une norme alors N'(0) = 0
qui donne N'(x) K* N(x) pour tout x appartenant à V
K* N(x) pour tout x appartenant à V
cela est-il correct pour prouver mon implication?
|N'(x) - N'(0)|
comme N' est une norme alors N'(0) = 0
qui donne N'(x)
cela est-il correct pour prouver mon implication?
Re: Montrer une implication entre deux normes
oui, exactement c'est pour ça que je ne comprenais pas.
mais (b) implique (c) comment tu as fait en 2mots?
mais (b) implique (c) comment tu as fait en 2mots?
Re: Montrer une implication entre deux normes
Pour (b) implique (c):
J'ai pour tout > 0 il existe
> 0 il existe  > 0 telle que N(x-y) <
> 0 telle que N(x-y) <  implique
implique
|N'(x) - N(y)| <
Je prend alors = 1
= 1
et je regarde N(( *(x-y))/(2*N(x-y))) c'est égale à
*(x-y))/(2*N(x-y))) c'est égale à  /2 qui est bien inférieur à
/2 qui est bien inférieur à 
J'ai alors que |N'(( *x)/(2*N(x-y))) - N'((
*x)/(2*N(x-y))) - N'(( *y)/(2*N(x-y))) | < 1
*y)/(2*N(x-y))) | < 1
avec les propriétés des normes, de la valeur absolue et enfin en factorisant j’obtiens
| N'(x) - N'(y)| < (2/ ) *N(x-y)
) *N(x-y)
J'ai pour tout
|N'(x) - N(y)| <
Je prend alors
et je regarde N((
J'ai alors que |N'((
avec les propriétés des normes, de la valeur absolue et enfin en factorisant j’obtiens
| N'(x) - N'(y)| < (2/
Re: Montrer une implication entre deux normes
Bonjour
(b) implique (c) ne me semble pas correct. En effet tu utilises que N' (l'application de (b)) est uniformément continue. Alors que dans (b) on ne sait seulement que N' est continue.
C'est à dire que pour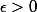 le nombre
le nombre 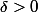 peut dépendre de x ou de y.
peut dépendre de x ou de y.
(b) implique (c) ne me semble pas correct. En effet tu utilises que N' (l'application de (b)) est uniformément continue. Alors que dans (b) on ne sait seulement que N' est continue.
C'est à dire que pour
Re: Montrer une implication entre deux normes
Bonjour,
Oui je vois que tu veux dire je me rappelle m'être fais la réflexion mais que par fainéantise ne pas avoir changer le x après avoir commencer avec et t'avoir écris vite ce que j'avais fais sans réfléchir. Je refait tout ça.
N' (l'appiation de (b) ) continue
Pour tout x pour tout > 0 il existe
> 0 il existe  > 0 telle que pour tout y N(x-y) <
> 0 telle que pour tout y N(x-y) <  ==> | N'(x) - N'(y)| <
==> | N'(x) - N'(y)| < 
Je pose x = 0 et je remarque que
N(( *(0-y))/(2*N(0-y))) = N((
*(0-y))/(2*N(0-y))) = N(( *(y)/(2*N(y))) =
*(y)/(2*N(y))) =  /2 <
/2 < 
La continuité me donne en posant = 1
= 1
| N'(0) - N'(( *y)/(2*N(y))) | < 1
*y)/(2*N(y))) | < 1
ce qui donne
N'(y) < (2/ )N(y)
)N(y)
je pose y = u - v et j'applique l'inégalité triangulaire
| N'(u) - N'(v)| < (2/ )N(u-v)
)N(u-v)
et ainsi ne dépend ni de u ni de v
ne dépend ni de u ni de v
Est-ce correct ainsi ?
Oui je vois que tu veux dire je me rappelle m'être fais la réflexion mais que par fainéantise ne pas avoir changer le x après avoir commencer avec et t'avoir écris vite ce que j'avais fais sans réfléchir. Je refait tout ça.
N' (l'appiation de (b) ) continue
Pour tout x pour tout
Je pose x = 0 et je remarque que
N((
La continuité me donne en posant
| N'(0) - N'((
ce qui donne
N'(y) < (2/
je pose y = u - v et j'applique l'inégalité triangulaire
| N'(u) - N'(v)| < (2/
et ainsi
Est-ce correct ainsi ?
Re: Montrer une implication entre deux normes
Oui c 'est ça mais à peu près. "à peu près" veut dire que la rédaction est lourde.
Re: Montrer une implication entre deux normes
Ok je tente en plus simplifier
On suppose N' continue
Pour tout x pour tout > 0 il existe
> 0 il existe  > 0 telle que pour tout y N(x-y) <
> 0 telle que pour tout y N(x-y) < ==> | N'(x) - N'(y)| <
==> | N'(x) - N'(y)| < 
Je pose x = 0 et = 1, on a alors que N(y) <
= 1, on a alors que N(y) <  ==> N'(y) < 1
==> N'(y) < 1
Pour u différent de v
Je pose y = ( *(u-v))/(2*N(u-v)) ==> N(y) =
*(u-v))/(2*N(u-v)) ==> N(y) =  /2 <
/2 < 
On peut alors appliquer la continuité ce qui donne N'(u-v) < (2/ )*N(u-v)
)*N(u-v)
On obtiens alors le résultat souhaiter en appliquant l'inégalité triangulaire
|N'(u)-N'(v)| < (2/ )*N(u-v)
)*N(u-v)
On suppose N' continue
Pour tout x pour tout
Je pose x = 0 et
Pour u différent de v
Je pose y = (
On peut alors appliquer la continuité ce qui donne N'(u-v) < (2/
On obtiens alors le résultat souhaiter en appliquant l'inégalité triangulaire
|N'(u)-N'(v)| < (2/
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
