Montrer qu'une expression est un entier
14 messages
- Page 1 sur 1
 montrer qu'une expression est un entier
montrer qu'une expression est un entier
Bonjour, je bloque sur une question (je n'arrive pas à trouver où insérer une racine cubique) :
montrer que A= racinecub(45-29*racinecar(2)) + racinecub(45+29*racinecar(2)) est un entier
j'ai étudié différents points de l'expression, notamment si on considère racinecub(45-29*racinecar(2)) = X
et racinecub(45+29*racinecar(2)) =Y
X^3 + Y^3=90
XY= 7
j'ai essayé de développer (x+y)^3 pour simplifier les racines cubiques :
(x+y)^3 = x^3 + 3yx^2 + 3xe^2 +y^3
= 90 + 3xyx+3yxy
= 90 + 3*7*x + 3*y*7
= 90 +21x+21y
je bloque..
Quelqu'un pourrait il m'aider à avancer svp.. ?
montrer que A= racinecub(45-29*racinecar(2)) + racinecub(45+29*racinecar(2)) est un entier
j'ai étudié différents points de l'expression, notamment si on considère racinecub(45-29*racinecar(2)) = X
et racinecub(45+29*racinecar(2)) =Y
X^3 + Y^3=90
XY= 7
j'ai essayé de développer (x+y)^3 pour simplifier les racines cubiques :
(x+y)^3 = x^3 + 3yx^2 + 3xe^2 +y^3
= 90 + 3xyx+3yxy
= 90 + 3*7*x + 3*y*7
= 90 +21x+21y
je bloque..
Quelqu'un pourrait il m'aider à avancer svp.. ?
Re: montrer qu'une expression est un entier
Super, du coup:
(x+y)^3-21(x+y)=90
Posons A=x+y
A^3-21A-90=0
6 est solution évidente ! Et la seule racine réelle.
(x+y)^3-21(x+y)=90
Posons A=x+y
A^3-21A-90=0
6 est solution évidente ! Et la seule racine réelle.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
merci beaucoup, je n'avais pas pensé à poser a=(x+y)!
Edit : et du coup, comme A^3 est un entier, on en déduit que l'expression aussi, en disant que le cube d'un entier est un entier et réciproquement ?
Edit : et du coup, comme A^3 est un entier, on en déduit que l'expression aussi, en disant que le cube d'un entier est un entier et réciproquement ?
Re: montrer qu'une expression est un entier
Ben tu as même montré que A (le nombre dont il est question) est égal à 6!
A est un nombre réel (c'est ton expression de départ) qui vérifie A^3-21A-90=0
Or le seul nombre réel qui vérifie cela est 6. Donc A=6
A est un nombre réel (c'est ton expression de départ) qui vérifie A^3-21A-90=0
Or le seul nombre réel qui vérifie cela est 6. Donc A=6
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
On a : ^3 = a^3 + 3a^2b + 3ab^2+ b^3)
Calcule:^3=45-29\sqrt{2}) , essais d'identifier les termes, tu obtiendras un système d'équations avec
, essais d'identifier les termes, tu obtiendras un système d'équations avec 
Calcule:
Re: montrer qu'une expression est un entier
Razes a écrit: essais d'identifier les termes
Oulah, que veux-tu dire par "identifier les termes" sans parler d'extensions de corps?

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
Ainsi, c'est plus clair:Lostounet a écrit:Razes a écrit: essais d'identifier les termes
Oulah, que veux-tu dire par "identifier les termes" sans parler d'extensions de corps?
Facile à résoudre, non?
Modifié en dernier par Razes le 04 Sep 2016, 15:33, modifié 1 fois.
Re: montrer qu'une expression est un entier
Quel argument te permet d'identifier la partie "rationnelle/naturelle" et la partie "√2" (il en faut bien un...)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
Tu veux qu'on étudie l'ensemble des nombre de la formeLostounet a écrit:Quel argument te permet d'identifier la partie "rationnelle/naturelle" et la partie "√2" (il en faut bien un...)
Re: montrer qu'une expression est un entier
Par exemple oui :p Au moins de quoi voir que (1,√2) est une base de quelque chose. Non?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
Oui, mais au niveau supérieur, on a dépassé ce stade.Lostounet a écrit:Par exemple oui :p Au moins de quoi voir que (1,√2) est une base de quelque chose. Non?
Re: montrer qu'une expression est un entier
Razes a écrit:Oui, mais au niveau supérieur, on a dépassé ce stade.Lostounet a écrit:Par exemple oui :p Au moins de quoi voir que (1,√2) est une base de quelque chose. Non?
Cela va dépendre du niveau... Personnellement, c'est pas ce je trouve le plus facile les extensions de corps (ici c'est simple avec √2 mais c'est toute de suite plus embêtant avec plus de choses et des √2^(3) et des i et pour identifier dans les deux membres avec des bizarreries).
Bref, une petite justification peut-être suffirait je pense pour suivre la méthode que tu proposes.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: montrer qu'une expression est un entier
quand on travaille sur les entiers alors 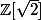 ou
ou  c'est la même chose
c'est la même chose
on a simplement un polynome en l'indéterminée avec la relation
avec la relation 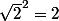
de même que est l'ensemble des polynômes en l'indéterminée i avec la relation
est l'ensemble des polynômes en l'indéterminée i avec la relation 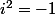
et c'est pourquoi cet ensemble de polynome est un espace vectoriel de dimension 2 ...

on a simplement un polynome en l'indéterminée
de même que
et c'est pourquoi cet ensemble de polynome est un espace vectoriel de dimension 2 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: montrer qu'une expression est un entier
La solution est doncRazes a écrit:Ainsi, c'est plus clair:Lostounet a écrit:Razes a écrit: essais d'identifier les termes
Oulah, que veux-tu dire par "identifier les termes" sans parler d'extensions de corps?;
Facile à résoudre, non?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
