Bonjour,
Voici l'exercice qui me pose problème :
X est une variable aléatoire de densité de probabilité fx définie sur IR par:
f x(t)=0 si t <2
f x(t)=a.t^(-4) si t≥2, a est un nombre positif.
Montrer que fx est une densité de probabilité, si et seulement si a = 24
Je ne sais pas comment m'y prendre.
Merci d'avoir lu, si quelqu'un peut m'éclairer svp
Montrer que fx est une densité de probabilité ssi a = 24
7 messages
- Page 1 sur 1
Re: Montrer que fx est une densité de probabilité ssi a = 24
Bonjour
Si c'est vrai, c'est que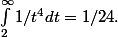
Tu peux commencer par faire ce calcul.
Si c'est vrai, c'est que
Tu peux commencer par faire ce calcul.
Re: Montrer que fx est une densité de probabilité ssi a = 24
Salut !
Il faut vérifier deux choses :
1. est continue par morceaux sur
est continue par morceaux sur  et,
et,
2. est positive sur
est positive sur  et,
et,
3. l'intégrale de sur
sur  tout entier vaut
tout entier vaut  :
: \ \mathrm{d}x=1) .
.
Remarque que est nulle sur
est nulle sur 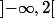 donc en fait la condition :
donc en fait la condition :
2. " est positive sur
est positive sur  " équivaut à "pour tout
" équivaut à "pour tout 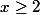 ,
, 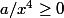 " donc
" donc 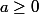 et,
et,
2. "\ \mathrm{d}x=1) " équivaut à "
" équivaut à "\ \mathrm{d}x=1) ". Or sur
". Or sur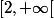 ,
, =a/x^4) donc il faut trouver
donc il faut trouver  tel que l'on ait :
tel que l'on ait : 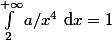 , ou encore
, ou encore 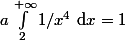 .
.

Il faut vérifier deux choses :
1.
2.
3. l'intégrale de
Remarque que
2. "
2. "
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Montrer que fx est une densité de probabilité ssi a = 24
Merci pour ces réponses, il me manque encore quelque chose pour bien comprendre :
Comment calculer une aire entre 2 et infini ?
J'ai tenté de poser un nombre t et calculer l'aire entre 2 et t et faire tendre t vers infini mais je n'obtiens rien de probant. Ce n'est pas la bonne méthode ?
Comment calculer une aire entre 2 et infini ?
J'ai tenté de poser un nombre t et calculer l'aire entre 2 et t et faire tendre t vers infini mais je n'obtiens rien de probant. Ce n'est pas la bonne méthode ?
Re: Montrer que fx est une densité de probabilité ssi a = 24
Il suffit d'intégrer de 2 à u puis de faire tendre u vers l'infini. Surtout ne pas prendre t comme borne d'intégration. t étant déjà la variable d'intégration
Re: Montrer que fx est une densité de probabilité ssi a = 24
sauvezmonannee a écrit:Comment calculer une aire entre 2 et infini ?
Il vaut mieux parler de "l'intégrale" entre
sauvezmonannee a écrit:J'ai tenté de poser un nombre t et calculer l'aire entre 2 et t et faire tendre t vers infini mais je n'obtiens rien de probant. Ce n'est pas la bonne méthode ?
Si c'est la bonne méthode : mais tu confonds les rôles de la variable d'intégration (que je note x) avec une des deux bornes de l'intégrale que l'on vers faire tendre vers
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Montrer que fx est une densité de probabilité ssi a = 24
Je vous remercie beaucoup pour ces précisions j'ai réussi l'exercice et bien mieux compris 
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
