Montrer que l'automorphisme intérieur est un endomorphisme

[Doraki]

tu as du oublier que x est pris dans G ?

et c'est pas "l'automorphisme intérieur" c'est "les automorphismes intérieurs", "les applications Int_x", "sont bien des automorphismes" etc.
parceque dans G il y a plein de choix possibles pour x.

[DamX]

x est pris dans G d'accord, mais en quoi cela assure que xgx^-1 est aussi dans G :/?

C'est quoi la définition d'un groupe ?

[DamX]

oui et qu'impliquent les propriétés de "l'inverse est dans G" et de la loi de composition interne sur xgx^-1 ?

[barbu23]

Bonjour, :happy3:

Le groupe est stable par multiplication qui est une loi de composition interne. Regarde la définition d'une loi de composition interne sur wikipedia.

Cordialement. :happy3:

[barbu23]

Salut :

Un ensemble est par définition, muni d'une loi de composition interne : et on note : si et seulement si : .
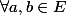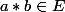Donc, désormais, si tu es devant un groupe quelconque muni d'une loi de groupe interne : , alors automatiquement, et sans réflechir : 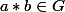pour tout : .

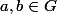Cordialement. :happy3:

Edit :

si on applique à deux éléments a et b appartenant à un ensemble E une lci *, alors a*b appartient à E, et il suffit de réitérer: si c appartient aussi à E, alors a*b*c aussi... en fait, on peut généraliser à l'infini, c'est ça?

Oui. :happy3:

[barbu23]

Ce que j'avais dit concernant la stabilité était il correct : "si par exemple on a deux éléments a et b d'un ensemble E et qu'on muni cet ensemble E d'une lci *, dire que cet ensemble est stable par cette lci revient à dire que a*b appartient aussi à E ?"
Bonne soirée

Oui. Cordialement. :happy3: