Salut,
Déjà, je pense que ça serait pas idiot de mettre des parenthèses dans ton truc pour le rendre clair :
\bigg))
implique que

est l'ordre de

(à la première lecture, je me suis dit que c'était n'importe quoi ton truc . . .)
Ensuite, c'est évidement faux ton truc vu que tout
diviseur 
de l'ordre de

vérifie la grande parenthèse, par exemple pour
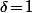
c'est forcément vrai.
Et en fait, ta grosse parenthèse, elle est équivalente à "

est un
diviseur de de l'ordre de

" et si tu veut un truc du style qui dise "

est égal à l'ordre de

", il faut prendre
)
Bref, pour montrer que

est l'ordre de

, tu ne coupera pas au fait qu'il y a
deux choses à montrer :
1) Que

(ce qui implique que
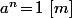
pour tout

multiple de

)
2) Qu'il n'y a pas de

(et
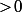
) tel que
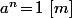
(sachant que s'il y en avait, il y en aurait forcément parmi les diviseurs de


