Montrer des inégalités

[jonses]

Bonjour ou bonsoir,

J'essaye de montrer des inégalités, mais ça fait un moment que je bloque.


---

Soit n>5

Je dois montrer que :


et


---

J'ai essayé d'utiliser des intégrales, d'exprimer le logarithme du binôme en somme, et de faire des études de fonctions, mais je pense que je m'y suis mal pris parce que j'aboutis pas du tout.
(je pense pas qu'une récurrence soit aussi efficace, enfin j'ai pas réussi par récurrence)



Si quelqu'un peut m'aider svp
Je vous remercie d'avance pour vos réponses

[adrien69]

Salut,
Tu connais pas d'inégalité sur ?
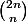
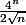
Compare avec et

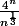
[jonses]

Salut,
Tu connais pas d'inégalité sur ?
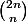
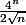
Compare avec et

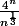
Désolé de dire ça, mais j'en connais pas sur

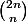
J'essaye de comparer ce que tu proposes, mais pendant ce temps ça m'a plus fait mal à la tête qu'autres choses, et puis je vois pas trop comment m'en servir pour aboutir au résultat

Merci en tout cas.

[jonses]

Salut,
Tu connais pas d'inégalité sur ?
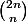
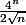
Compare avec et

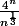
Désolé de dire ça, mais j'en connais pas sur

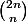
J'essaye de comparer ce que tu proposes, mais je vois pas du tout comment y arriver, et puis je vois pas trop comment m'en servir pour aboutir au résultat

Merci en tout cas.

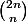
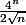
Au fait, est-ce qu'il faut vraiment que je compare à et ?

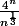
Parce que j'ai l'impression que c'est pas vraiment possible de les comparer, enfin perso j'ai beau chercher...

[adrien69]

Franchement, tu mets dans le logarithme et ça te donne la solution en deux lignes...
Et bon je t'ai donné un encadrement très serré, mais trouves-en un plus lâche par toi-même si tu ne vois pas comment montrer celui-ci.

[jonses]

Franchement, tu mets dans le logarithme et ça te donne la solution en deux lignes...

Désolé, mais j'ai essayé avec le logarithme, ça donne rien d'évident :



J'ai essayé, étude de fonction, encadrement par intégrale, majoration et minoration grossière de la somme... et perso j'aboutis à rien.

J'ai sûrement dû rater un truc, mais je trouve pas la solution en deux lignes

[Ben314]

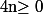
On montre facilement par récurrence que, pour tout , et je pense que ça doit suffire pour montrer tes inégalités.
S'il te faut "mieux", (toujours par récurrence) ,

[jonses]

Merci !

(Pourquoi je vois jamais les choses évidentes ! Raah ! :mur: Désolé, c'est juste que je bloque trop souvent sur des choses simples en math, ça devient assez énervant )

[adrien69]

Merci !

(Pourquoi je vois jamais les choses évidentes ! Raah ! :mur: Désolé, c'est juste que je bloque trop souvent sur des choses simples en math, ça devient assez énervant )

Ouais surtout que je t'avais donné un encadrement quasiment équivalent auquel il suffisait d'appliquer le logarithme comme je l'avais aussi suggéré...

[jonses]

Ouais surtout que je t'avais donné un encadrement quasiment équivalent auquel il suffisait d'appliquer le logarithme comme je l'avais aussi suggéré...

Je devais faire des erreurs de calculs à outrance, c'est pour ça à mon avis que j'arrivais pas à aboutir malgré ton indication (je pense qu'il faut faire un petit calcul après avoir passé au logarithme ton encadrement, non ?).

Bref depuis une semaine, j'ai l'impression que je suis pas dans le meilleur de ma forme...

Sinon merci encore !