Module de type fini !

par **barbu23** » 18 Fév 2009, 00:44

Bonsoir :
Soit

un

- module et

un sous module de

.
Je dois montrer que :

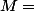
est de type fini

est de type finie où :

est la surjection canonique.
Voiçi comment je procède :
Soit :

un sous module de

tel que :

.
Alors :

est sous module de

qui contient

et donc :

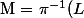et

Par contre je ne vois pas comment montrer que :

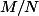
Il est clair que :

, il reste à montrer que :

Quelqu'un peut-t-il me donner un coup de pouce ?
Merci d'avance !

par **Doraki** » 18 Fév 2009, 00:49

L = ?

par **barbu23** » 18 Fév 2009, 01:00

Oui, et c'est ça ce que j'arrive pas à montrer la seule donnée que j'ai est que

, Mais pas :

malheureusement !
Merci d'avance de ton aide doraki ! :we:

par **Doraki** » 18 Fév 2009, 01:06

Tu as montré que pour tout sous-module L de M/N,
pi(S) inclus dans L => M/N inclus dans L (=, même)

Il suffit donc juste de choisir L = , nan ?

par **barbu23** » 18 Fév 2009, 01:32

J'ai encore du mal à comprendre ça doraki :
Non, ou est ce que j'ai montré ça :

Non, pas du tout !
Tu peux m'expliquer ça un peu en detail ! parceque je suis complètement perdu !
Merci d'avance !

par **barbu23** » 18 Fév 2009, 16:37

Ah ben maintenant, je comprends :
Tout sous module de

contenant

est égale à

et donc :

qui est un sous module de

contenant

est égale à

.
Cordialement !