Module libre engendrer par un element regulier?

[alihababi]

slt,
comment montrer qu'un idéal J est libre ssi J=xR tel que x est régulier?

[Ben314]

Salut,
Bon, déjà, vu que je suis francophone, l'anneau je vais l'appeler A et pas R.
Ensuite, je vais supposer (vu que hélas rien précisé) que A est un anneau commutatif unitaire (et donc qu'on parle forcément d'idéaux bilatères).

Sinon, dans le sens xA; a->xa est bijective donc J, vu en temps que A-module est libre (de base {x})
Pour la réciproque, si J est un A-module libre alors il possède une base B (définition) donc tout élément j de J s'écrit de manière unique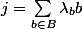 où les sont dans et sont tous nuls sauf un nombre fini d'entre eux.
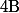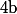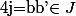Si contenant deux éléments distincts et alors l'élément pourrait s'écrire 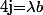avec 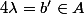mais aussi 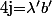avec 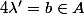ce qui contredirait l'unicité sus décrite (je sais pas si ça se dit, mais ça fait sacrément classe je trouve :marteau: )
Donc, (en supposant qu'on ne considère pas {0} comme un idéal donc que B est forcément non vide) , on a forcément B={x}, c'est à dire J=xA et le fait que xA est libre montre immédiatement que x est régulier.