Module et complexe

[dalman]

Bonjour à tous,
alors voila j'ai un exercice à préparer mais je ne sais pas par ou commencer.
Voici le sujet:
" Déterminer tous les complexes z tels que module z= mod(1/z)=mod(1-z)
On donnera les solutions sous forme algébrique puis sous forme exponentielle . "

Je ne comprends pas ce qu'il faut faire au juste.
Merci d'avance

[euler21]

salut
si tu as |z|=|1/z| alors nécessairement |z|²=1 ..

[Purrace]

y'a d'autres egalité a prendre en compte , ca reduit l'ensemble des solutions

[dalman]

oui j'en été aussi venu a ce moment la mais je ne sais pas quoi en faire après.

[abcd22]

Bonsoir,
Puisqu'on dit de donner les résultats d'abord sous forme algébrique, écrire z = a + ib, puis calculer |1-z| en fonction de a et b.
Sinon on peut le voir géométriquement : z est sur le cercle unité, donc -z aussi, et (-z) + 1 aussi puisque |1-z| = 1, donc les valeurs possibles pour (-z) + 1 sont les affixes des points d'intersection du cercle unité et du cercle de centre le point d'affixe 1 et de rayon 1, c'est-à-dire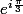 et (justifier), en enlevant 1 et en prenant l'opposé (symétrique par rapport à O) on voit qu'on retombe sur ces mêmes points. Enfin c'est une explication qui est bien à l'oral mais dans une copie c'est sûrement plus rapide de faire le calcul algébrique.

[Ben314]

Salut,
Il est aussi de bon ton de constater que, si z est l'affixe d'un point M et que l'on note O et A les points d'affixes 0 et 1 alors |z|=OM et |1-z|=AM donc les complexes tels que |z|=|z-1| sont ceux situés sur...

[dalman]

sur la mediatrice du segment [OA]!! ok pour ça!!

mais abcd22 je n'arrive pas a retrouver des exponetielle. Comment a tu fais??