Module et arguments d'un nombre complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 18:10
par Izio38 » 16 Nov 2016, 18:10
Bonsoir,
Ayant un DS demain, et n'arrivant pas à résoudre un simple exercice, je cherche de l'aide pour trouver le module et l'argument du nombre suivant :
})
Merci d'avance !

Bonne soirée
Modifié en dernier par
Izio38 le 16 Nov 2016, 19:36, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 18:25
par Ben314 » 16 Nov 2016, 18:25
Salut,
C'est quoi la définition du module d'un nombre complexe

?
Et c'est quoi la définition d'un argument de

?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Nov 2016, 18:27
par zygomatique » 16 Nov 2016, 18:27
salut
niveau supérieur ?
je ne vois rien de gênant lorsqu'on sait ce qu'est le module et l'argument d'un nombre complexe
EDIT : grillé ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 18:29
par Izio38 » 16 Nov 2016, 18:29
Je sais très bien le calculer d'habitude mais la c'est un nombre particulier dans le sens que nous ne savons pas les trouver avec nos méthodes.
Module de z : V (x^2 + x^2)
Et argument trouvable avec cos (O) = .... et sin (O)=....

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 18:33
par Ben314 » 16 Nov 2016, 18:33
Izio38 a écrit:Module de z : V (x^2 + x^2)
Et argument trouvable avec cos (O) = .... et sin (O)=....
Effectivement, si c'est ce genre de charabia où on ne sait même pas ce que représentent les lettres présentes que tu appelle une "définition", ben c'est sacrément mal barré.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 18:40
par Izio38 » 16 Nov 2016, 18:40
Pour z appartenant à l'ensemble C (complexe) z = x + i × y = 1 + i ( 1 + racine (2) )
Je sais que le module de z est la distance entre le centre du cercle trigonométrique et z et que on pose le module de z = racine(x^2 + y^2)
D'autre part l'argument est l'angle entre le nombre 1 et le nombre z sur le cercle trigonométrique et on pose cos (O) = x/r et sin(O) = y/r
O étant la lettre grec téta
r étant le module
Je recherche juste un peu d'aide la dedans car j'ai le module j'ai le cos et sin mais je n'arrive pas à trouver l'argument.
Pour le carré du module j'ai 4 + raxine(2), j'ai fais la quantité conjuguée pour cos(O) mais il n'a pas l'air comode ^^
J'ai mis au carré car sinon le module semble ( à mon niveau) être inutilisable

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 18:57
par Ben314 » 16 Nov 2016, 18:57
Le module de

c'est

(et pas

) et ça ne se simplifie pas.
Par contre, le fait que
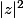
soit "plus simple" que
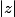
, ben ça devrait t'inciter à commencer par chercher un argument de
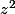
pour
ensuite en déduire un argument de

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 19:02
par Izio38 » 16 Nov 2016, 19:02
Oui pardon c'est ce que j'ai eu en plus mais je l'ai mis au carré donc j'ai trouvé cos^2 (O) = 1 / (4 + 2* racine (2)) mais même en faisant la quantité conjugue je fini par cos^2 (O) = ( racine(2) + 2) / 4 et c'est cette chose qui m'embête car je ne connais aucune valeur similaire et je ne sais pas comment me retrouver à quelque chose de plus simple
Je te remercie de ton aide
ÉDIT : en fait j'ai cos^2 (O) = ( 2 - racine (2) ) / 11
Et pour sin^2 (O) = racine (2) / 11
Modifié en dernier par
Izio38 le 16 Nov 2016, 19:12, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 19:10
par Ben314 » 16 Nov 2016, 19:10
Est-ce que ce que je t'ai dit de faire c'était d'élever cos(theta) et sin(theta) au carré ou bien c'est autre chose que j'ai dit ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 19:16
par Izio38 » 16 Nov 2016, 19:16
Ah oui je met z au carré je trouve le module que tu as donné mais sans la racine puis je met sous la forme cos(theta) et je trouve les valeurs que je t'ai donné. Mais le problème est pour trouver l'argument de z carré car après je n'aurais qu'à le diviser par deux pour avoir l'argument de z d'après la définition de la forme exponentielle
Édit : je vais sur le PC pour te montrer ce que j'ai trouvé avec l'éditeur d'équation ça sera plus lisible peut être

Edit 2 :


 = \sqrt{\frac{2 - 2 \sqrt{2} -11}{11}} })
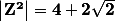
et je sais que :
 = \cos ^2 (\theta) +1 })
donc que :
 = \sqrt{\cos(2\theta) -1} })

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 19:34
par Ben314 » 16 Nov 2016, 19:34
Je trouve... absolument pas ça du tout... (à part le module)
Tu as trouvé quoi pour
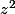
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 19:39
par Izio38 » 16 Nov 2016, 19:39
C'est assez rassurant pour moi vu que j'ai DS demain :'D
Alors pour

, j'ai :
 + i \sin (\theta))})
Si je remplace théta, j'ai :
 + i (\frac{\sqrt2}{11}))})
Modifié en dernier par
Izio38 le 16 Nov 2016, 20:52, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 19:54
par Ben314 » 16 Nov 2016, 19:54
Je te demande pas une écriture théorique, mais bien plus simplement combien ça vaut
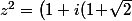\big)^2)
quand on développe le carré.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 20:35
par Izio38 » 16 Nov 2016, 20:35
Je trouve cela

et au passage j'ai compris là où tu souhaitais en venir. En fait je prenais la partie Réelle de Z et non de Z² pour calculer l'argument. J'essaye de suite. Merci encore.
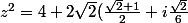)
Donc pour z :
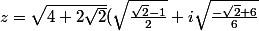)
Mais comment trouver le theta correspondant à ces valeurs ? Car que ce soit pour z ou pour z², je ne connais pas ces valeurs ... J'ai beau refaire le calcul 2/3 fois, je retombe dessus.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Nov 2016, 13:23
par zygomatique » 17 Nov 2016, 13:23
z^2 est faux ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 17 Nov 2016, 15:15
par mathelot » 17 Nov 2016, 15:15

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Nov 2016, 19:59
par zygomatique » 17 Nov 2016, 19:59
pourquoi faire compliqué quand on peut faire simple ... quand on sait calculer ...
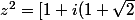]^2 = 1 - (1 + \sqrt 2)^2 + 2i(1 + \sqrt 2) = -2 - 2\sqrt 2 + 2i(1 + \sqrt 2) = 2(1 + \sqrt 2)(-1 + i))
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités