Minimum d'une fonction

par **nemesis** » 04 Juin 2007, 20:55

bonsoir
comment faire pour determiner le minimum de la fonction suivante

sous la contrainte

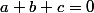
juste la methode svp
merci d'avance .

par **Joker62** » 04 Juin 2007, 21:04

Considérer l'espace vectoriel des fonctions continues sur [-1;1]

Munir cet espace du produit scalaire intégrale de -1 à 1 de f(t)g(t) dt

Et étudier le projeter orthogonale de sin (pi t) sur le sous espace des polynômes de second degrés ;)

par **nemesis** » 04 Juin 2007, 21:17

et ou est ce qu'intervient la contrainte?

par **Joker62** » 04 Juin 2007, 21:51

Le truc c'est que tu vas devoir résoudre un système de deux équations à 3 inconnus pour trouver a, b et c
Et le truc, c'est que a + b + c te permettrons de conclure :)

par **fahr451** » 04 Juin 2007, 22:09

bonsoir
"la contrainte" permet de se placer d'emblée dans un plan ( garder a et b par exemple)et de faire ce qu 'a dit joker

par **quinto** » 05 Juin 2007, 01:08

Sinon si ça t'amuse, tu peux considérer la fonction de 3 variables a,b,c et utiliser les multiplicateurs de Lagrange mais c'est vraiment débile de faire ceci ici.

par **Joker62** » 05 Juin 2007, 01:21

Lol ouai un tit peu :D
Enfin, c'est une autre solution quoi ;)

Minimum d'une fonction

minimum d'une fonction

Qui est en ligne