Minimum de ||.||_2 sur SLn(R)

[yos]

Bonsoir à tous.

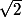
C'est un exercice facile et intéressant (niveau L1-L2) de montrer que le minimum de la norme euclidienne sur est et que ce minimum est atteint sur (et uniquement là).
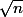
J'ai envie de dire que le minimum de la norme euclidienne sur est . Qu'en pensez-vous?
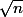
Il est déjà évident que cette valeur est atteinte sur Mais je ne vois rien de plus.

[tize]

Salut Yos,
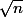
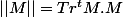ok pour moi, le minimum est bien avec pour en utilisant les multiplicateurs de Lagrange...

[yos]

Les multiplicateurs de Lagrange? Où les ais-je fourrés? Intéressante initiative en tout cas. Merci pour ta réponse. Je vais voir ça.

[tize]

Oui effectivement j'ai oublié le carré....merci pour la correction :we:

[ThSQ]

Intéressant, dommage que j'ai ce fo*tu DM de 20 pages de physique à finir :marteau:

Une idée comme ça avant d'aller se coucher (pas taper si c'est idiot) : est invariante si on remplace M par OM, O orthogonale. En utilisant la décomposition en valeurs singulières ( http://fr.wikipedia.org/wiki/D%C3%A9composition_en_valeurs_singuli%C3%A8res ) est-ce qu'on peut pas se ramener à une matrice diagonale ?

[yos]

Génial! Plus qu'à conclure avec l'IAG. Bravo et merci.
Voilà donc deux bonnes solutions.