Minimum global

[NAJMA]

Salut
La fonction f:R^n-->R continue telle que
Lim f(x) =+infini
x-->+ infini
Alors f admet un minimum global
Je veux montrer ça
J'ai utilisé la définition du limite en plus infini mais je me suis bloqué.

Cordialement

[guillaume100]

Bonsoir,
Ta fonction elle part de R non ? ou de R^n ?
Sinon il manque une hypothèse sur f: la fonction f qui à x associe x^3 a pour limite +infini quand x—>+infini mais admet pas de minimum global car elle a pour limite -infini quand x—>-infini,

je pense que l’hypothese Est que f vaut +l’infini quand x—> +infini ou -infini non ?

De là tu peux découper R en 3 intervalles bien choisis et utiliser un certain théorème des fonctions continues sur un segment pour un des intervalles, et la définition de la limite qui vaut +infini pour les 2 autres

[mathelot]

bonjour,
pour tout réel A, il existe un réel B>0 tel que
|x| > B f(x)>A
on choisit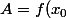 pour un fixé.

l'ensemble F={x / |x| B} est fermé , borné donc compact (espace vectoriel normé de dimension finie)
f est minorée sur F et atteint son minimum. notons m ce minimum.
il existe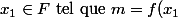
Soit ). f est minorée par M sur ou
et atteint son minimum car A et m sont des images par f.

[NAJMA]

D'accord merci á vous
Cordialement